有的家长常常会苦恼:为什么孩子数学总是学不好?
这个问题其实很复杂,首先是标准问题,何谓“不好”,你定义的“不好”是什么标准?每个人的标准可能不一样,甚至不少家长认为孩子不好,其实没有标准,就是一种直觉。
然后,我们去探讨数学学不好的原因。而这也就是本文的主要内容。
人所共知,没有良好的学习态度,主观上不想学好,那谈什么都没用。至于兴趣,爱因斯坦的名言同样为大家所认可:兴趣是最好的老师。所这里让我先排除态度和兴趣问题。
在态度在线,不抗拒数学(因为要有兴趣真不容易)的前提下,为什么数学依然学不好?
“不好”的具体表现可能是以下两个完全相反的方面:
第一,极其粗心,低级错误非常频繁,说什么就是改不了。比如经常初算计算多个0少个0,拆(添)括号忘记变号,上一步正常下一步抄错数字,看漏题目条件等等乱七八糟的奇怪错误。
第二,做题慢效率低。可以是慢到7×9都要呆一下,100-30都要用竖式的那种。这类学生,差不多就是前面一类学生的反向存在,经常练习的,该做对的都能给你做对,但一上难度就蒙圈。
这两种表现是表象的,可见的,还有一个问题,一般家长可能说不上来,那就是缺乏联系性和想象力。
如果不追求竞赛或者升学加成,只要态度端正,认真听课,完成老师布置的作业,课内成绩可以很漂亮。但缺乏联系性和想象力会导致的问题,在初二开始将逐渐展现,随着数学知识的广度和深度增加,会愈发明显。
这时候,数学会出现一个叫做“压轴题”的玩意儿。压轴题就是拿来区分优秀学生和顶尖牛蛙的,它是带着使命出现在这个世界的。
压轴题当然不是一蹴而就的,平常不怎么接触,考试忽然会做,几乎不可能。因此,身处优秀班集体的学生会跑在前头,原因是老师讲得多,当然,找到合适的有针对性的课外辅导也可以起到部分作用。
但是,压轴题这玩意也不是讲得多就会,更不是谁都能会,它对学生学习能力的要求很高。缺乏联系性和想象力,无论多努力,都会遇到瓶颈。毕竟,这个世界终究是看能力大小而不是看努力的多少。
数学难题说白了就是变化多端,考点繁多,深度充足的。单一知识点不足以解决问题,解决一道数学难题需要“分析条件——思考考点——联系过往类似的题型——结合该题的特征”。
分析条件:这句话想让我干啥?
思考考点:我该用什么学过的东西来入手?
联系旧题:这些条件(包括图)的组合有没有和我以前做过的某道(类)题很相似?
结合本题:那道题是怎么解的,本题和那道题的区别(条件差异)是什么?
例如刚结束的2021年广州中考数学卷24题:

第(2)问的“最高处”,指向的是顶点纵坐标,于是配方或者公式求顶点;
第(3)问已知E、F两点,遂求一次函数解析式,“一个交点”指向联立方程求解或△=0,这都是分析条件和思考考点后应该得出的结论,应该拿到的分数。
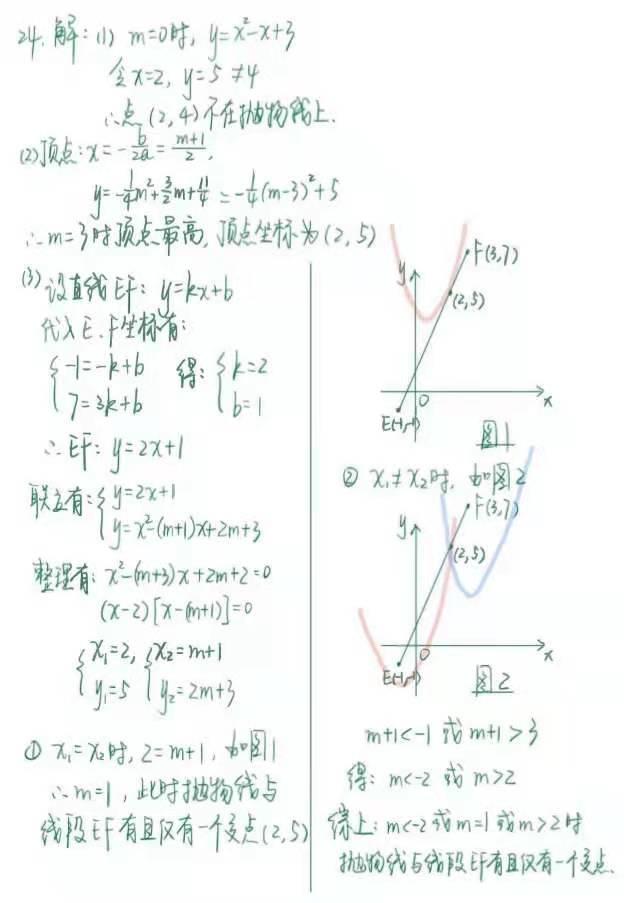
涉及函数交点联立方程的做法,是固定思路,学生必定做过多次。而联立方程后的分类讨论,则是因为该题的特性,即EF是线段,要思考线段与直线在处理上的不同之处,这就是上面提到的要综合过往题目的“共性”与本题的“特性”。
事实上,很多学生在学习的时候,没有把新学知识和原有内容有意识地结合起来,部分老师可能也疏忽了这一点,缺乏引导,而是单独地教授新知识。

初中第一年,每一个章节都是在打基础,上图标红的六章书,都是在为日后的计算打下基础,他们共同构成了所有理科能力里面一个最重要的部分——运算能力。
同理,第四章《几何图形初步》以及第五章《相交线与平行线》是线和角的初步认识,是几何的开端,第七章《平面直角坐标系》是函数重要的前置知识。
这些内容,单独拿出来都不难,因此小学课内基础过关,学习态度认真的学生,普遍学得不错。虽然中考单独出题也不多,但你能说他它们不重要吗?
整式学不好,初二的因式分解、分式就会吃力,平面直角坐标系不过关,初二下学期起开启的函数之路必然不会顺畅,这条路除了包括初中的一次函数、二次函数和反比例函数,还包括高中的函数性质、基本初等函数、三角函数,乃至解析几何,圆锥曲线。
多思考新知识和旧知识之间的关联性,你就会发现,出现在高一课本上的一元二次不等式,其实不过是初中二次函数图像的变形,根本都算不上什么新知识。
多思考新题目和旧题目之间的关联性,你就会发现,每一道新题的某一部分都是自己以往见过的,旧瓶换新酒。
要知道,大考出题者也是很艰难的,知识也就那些,在不能超纲的前提下,如何把固有考点玩出新花样,也是挠破头的事情。
至于想象力,那更是现代人的稀缺资源。充足的想象力,能够在脑中构建起一幅一幅的图像,在函数问题,立体几何,解析几何里就会事半功倍。这一点,我国著名数学家华罗庚甚至曾为此赋过一首诗:

这两项能力的缺失,可能就是很多孩子数学桎梏的内因。但是,我们的教育却显得不够重视,甚至一直扼杀着学生的这两项能力。
过度的超前学习,硬塞的奥数知识,不理解原理却被要求背诵的公式,执着于“xx模型”的套路化解题,一些知名线上机构广告里常常宣扬的“xx个解题大招”……这些都是具体表现。
风清扬说过:“活学活使,只是第一步。要做到【出手无招,那才真是踏入了高手的境界】。金庸笔下武侠的最高境界,大概就是解题的最高境界。

但是我们毕竟要应对考试,记忆的重复训练依然是短期提高的最佳做法。既然是最高境界,能达到者也寥寥,不要说学生,老师也是如此,题目日新,老师也要不断精进。
但是我们日常可以有意识地尝试,每学习一个新知识,或是遇到新题目的时候,首先思考一下有哪些地方和我脑海中某个角落里的东西有点像,进而把它调取出来比对。这大概也是“带着脑子学习”的一种具体表现吧。
,




