数学准备
- 雅可比矩阵(Jacobian):向量对向量的偏导数所构成的矩阵,考虑函数从空间映射到另一个空间(
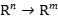
- ),则雅可比矩阵形成一个m行n列的矩阵,矩阵元标记为
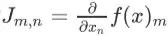
- 。
- 海森矩阵(Hessian):一阶导数的雅可比矩阵,因为二阶偏导的连续性,可以交换偏导的先后顺序,所以海森矩阵也是实对称矩阵。
- 方向导数(direction derivative):某个标量对特定方向d(单位向量)上的导数,度量了该标量沿着该方向的变化率,是一个向量。
- 梯度(Gradient):变化率最大的方向导数。
- 鞍点(saddle point):Hessian正定,对应局部极小值,Hessian负定,对应局部最大值,Hessian不定,对应鞍点(注意,这是充分非必要条件)直观来看,鞍点就是一个方向上是极大值,另一方向却是极小值。
- 厄米矩阵(Hermitian):对称矩阵的复数域扩展,实对称矩阵是厄密矩阵的特例。厄米矩阵可以被对角化。
- 特征值:矩阵做对角化变换前后,特征向量被缩放的比例。特征向量和特征值是矩阵的固有属性。

在开始深度学习之前,我们要对深度学习和统计学习的重要工具——优化算法——做一个全面深刻的剖析,首先我们要问:机器学习为什么要使用优化算法呢?举个例子,普通最小二乘的最佳参数表达为:

虽然我们可以获得解析表达,但是当数据量变得非常庞大的时候,连计算矩阵的逆都会变得非常慢。同时在很多情况下,我们无法获得参数的解析表达,就需要采用迭代的方式逼近最佳的参数值。
迭代的方式有很多种,比如坐标下降法(coordinate descent),它的想法很简单,将变量分组然后针对每一组变量的坐标方向最小化Loss,循环往复每一组变量,直到到达不再更新Loss的坐标点。但即便这样,坐标下降法仍然迭代的非常缓慢,很大一部分原因在于它的搜索方向是固定的,只能沿着坐标的方向,而这样的方向并不能保证是最快的。同时,坐标下降需要假设变量之间的影响非常微弱,一个变量的最优不会影响到另一个变量的更新,但这一条件往往很难满足。

图为坐标下降应用到两个参数构成的Loss,我们可以发现,参数只在两个垂直的方向上进行更新,这是因为我们看到的contour就处在两个参数构成的直角坐标系中,分别对应着坐标的方向。
相较于坐标下降,基于梯度是所有方向导数中变化最快的,梯度下降(gradient descent)也被叫做最速下降,对机器学习有些许了解的同学会很容易写出梯度下降的公式:
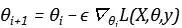
首先,Loss function一般都是标量,它的雅可比矩阵就是一个列向量,其梯度指明了下降的方向,说明沿Loss梯度方向更新参数会得到最大程度的改变,学习率是一个标量,与梯度相乘,指明了下降的幅度。

图为梯度下降在两参数构成的Loss,可以发现,参数会沿着垂直于contour的方向进行更新,垂直于contour的方向正是梯度的方向。
Hessian中包含了Loss function的曲率信息,因为Hessian可以理解为梯度的雅可比,一个函数的导数衡量的是函数的变化率,所以Hessian衡量的就是梯度的变化率。同时Hessian矩阵由于是厄米矩阵,可以被对角化,它的特征值和特征向量可以分别定义为:
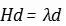
如果特征向量被正交归一化,那么特征向量d就是基,那么特征值就是该方向上的二阶导数,两边同时乘以特征向量的转置,就可以得到:
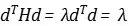
比如对于鞍点,某个特征向量所对应的特征值就是负的,就意味着是这个方向上的极大值点,而另一特征向量所对应的特征值就是正的,意味着同时也是另一方向上的极小值点。从数学上来说,鞍点的来源是极大值极小值都要通过导数为零得到,但不同的方向导数定义在了不同的维度上。
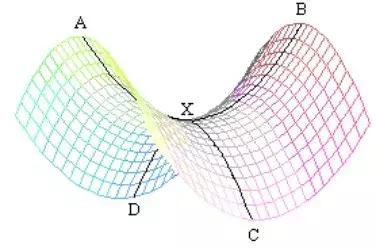
如图,AB方向和CD方向,二阶导数的正负并不一致,产生了X这样一个鞍点。
其余的方向的二阶导数就可以通过特征向量来计算,因为特征向量可以构成一组基(完备正交),所有向量都可以用这组基进行线性表示,任意方向f可以被表示为:

所以,任意方向的二阶导数都可以得到:

Hessian能够告诉我们非常重要的一点,随着参数点的不断更新,梯度会如何变化。举个例子,在很多教材上都会讲学习率的设定,学习率如果过大,就会在很大的Loss附近震荡,如果太小,需要迭代的次数又太多。

如图,不同的学习率会对梯度下降的性能造成影响。
那么,多大的学习率才合适呢?具体到这个例子上,这明显是一个凸函数(特指向下凸),代表着梯度会变得越来越小,也就是说固定好学习率的前提下,随着参数点的下降,我们下降的会越来越慢,我们将Loss function做泰勒展开:
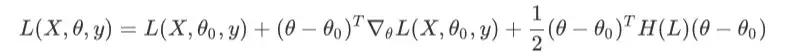
假设从
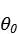
到

,我们执行了一次梯度下降,那么就有关系:
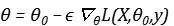
将梯度

表示为g,其带入泰勒展开式,可以得到:
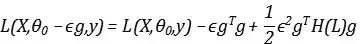
如果我们将后面两项写作一项:

如果中括号里面的项大于零,那么Loss 总会减小,比如Hessian的特征值均为负,其实对应着极大值点,那么无论学习率多小,Loss总会下降很大。但是,如果Hessian特征值均为正,而且非常大,就意味着极小值附近的曲率非常大,那么执行梯度下降反而会导致Loss的上升。如果我们希望Loss能下降最多,其实就是希望中括号项越大越好,在Hessian特征值为正的情况下,在我们将看作变量,令其一阶导数为零,这样就求到了极大值(因为在Hessian特征值为正的前提下,二阶导数小于零):

就可以得到:
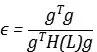
就给出了我们的最优步长。同时,我们可以将Loss function做泰勒展开,展开到二阶:
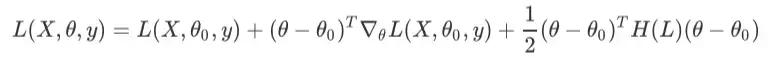
考虑到一阶导数为零的点对应着极值点,我们对上式求一阶导数,并令其为零可得:

这样就得到了牛顿法(Newton method)的更新公式。牛顿法已经默认使用了一阶导数为零的信息,理想情况下,它只需要从初始参数点迭代一次就可以找到极小值点。同时,它利用了Hessian中的曲率信息,一般而言也要比梯度更快,在下降方向上并不是梯度的方向,从数学上可以看出Hessian乘以梯度,本质上会得到Hessian特征向量的线性叠加,如果梯度恰好作为了Hessian的特征向量,那么牛顿法和梯度下降的下降方向才会一致。
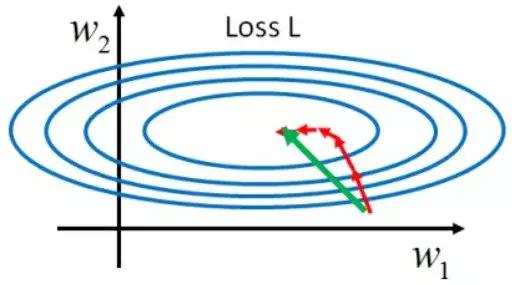
如图,红线表示梯度下降的路径,绿线表示牛顿法的路径。

读芯君开扒
课堂TIPS
这里着重强调:优化算法的快慢和计算代价是两回事情。优化至局部最小值所需要的迭代次数越少,就可以说优化地越快。梯度下降比坐标下降快,牛顿法比梯度下降更快,但我们可以非常容易的看到,在每次迭代时,梯度下降需要计算全部样本的梯度,牛顿法甚至需要计算全部样本的Hessian,虽然迭代次数减少了,但每次的计算代价却增加了。

作者:唐僧不用海飞丝
如需转载,请后台留言,遵守转载规范
,