网友:一个巨大的小行星以恰好的速度和力度撞击地球,逼停其绕太阳的公转。地球要过多久才会跌进太阳?
回答:这个问题有两种解决方式……一个是咬紧牙关解微分方程,代入数值,得出答案。另一个,是使用已知的量和与轨道相关的知识来解。
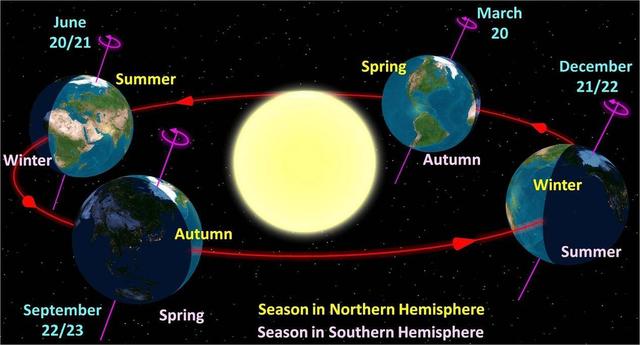
图解:地球在其轨道上的季节点(不按比例)
对太阳没有角动量的物体的运动方程,描述如下:
r'' = -GM/r2
[G是重力常数,M是太阳质量,r是物体到太阳的距离]
其中质数表示与时间有关的差异,一个会进行两次积分,第一步是:
r' = - √(2GM) * √(1/r - 1/R)
当R代表距太阳的最初距离时,在这里它就表示从太阳到地球的距离

图解:地球到太阳的距离的图示。
第二次积分需要一点技巧,但还是可行的,它能得出以下方程:
r*R*√(1/r - 1/R) R3/2arctan(√(R/r -1)) =√(2GM)*t
在这里,t是物体在R距离中运动的时间。现在我们想要找到当r为0时的t值,这实际上比看起来要简单。左边的第一项消失了,反正切函数的参数变成了无限大,而无限的反正切值是π/2,经过处理之后,我们得到:
t = √(
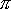
2*R3/(8*G*M))
这个到达太阳的时间,有没有忽略太阳自身的运动和太阳自身的体积呢?
我们如何估算这个值?地球绕太阳运动的周期可以由这个公式得出:
T = √(4*
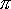
2*R^3/(G*M))
当然了,这个答案是一年。
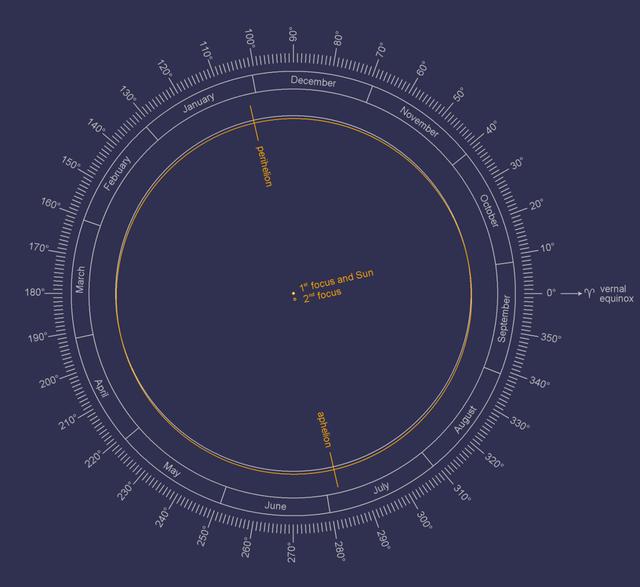
图解:地球轨道(黄色)与圆(灰色)相比
比较这两个,我们可以发现:
t = T/(4*√(2))
大概是64天零12小时,或者两个月多一点的时间与这个残酷的世界告别,然而,到最后可能会很热。
现在,是另一个,涉及数学更少而偏物理的方法。
我们知道任何轨道的周期都只与半长轴有关,只要它是一个椭圆且太阳位于其中一个焦点。
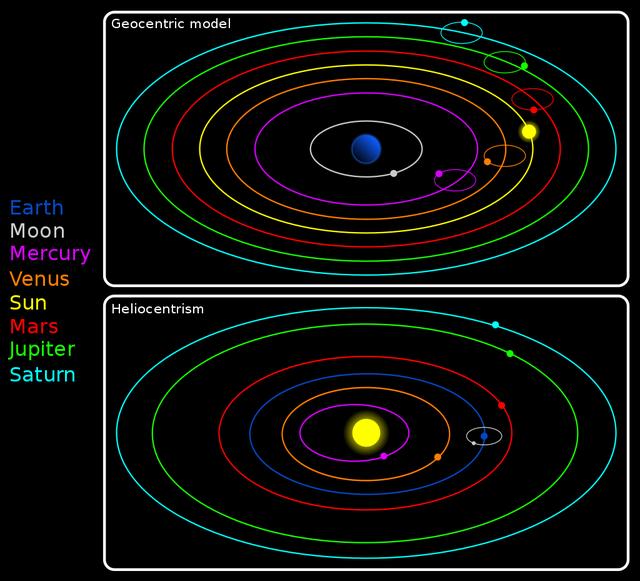
图解:与地心模型(上面板)相比的日心(下面板),不按比例
我们可以将这个问题看成轨道是一个极平的椭圆。将焦点放在一端,而物体从另一端开始运动。所以在这里我们只需要计算轨道的半个周期,因为半长轴就是R的一半,如果你继续算的话会发现。
所以表达式就是:
t = (1/2)*√(4*

2*(R/2)3/(GM))
简化之后是:
t = (

2*R3/(8*G*M))
与之前的表达式相同。

图解:季节和地球轨道的一些特征。椭圆的形状被强烈地夸大了。
另外需要说明的是,小行星的质量在方程中并不考虑,只要它没有大到在碰撞后能使地球的质量可以和太阳的质量相提并论,这时候我们才需要在推导过程中考虑太阳的运动。(这可以通过使用减少后的质量来维护,但那又是另一段说法了)

图解:太阳系重心相对于太阳的运动
你提出的小行星需要自身动量与地球质量乘以轨道速度相同,但方向相反。具体来说就是另一个以18英里/秒速度运行的和地球大小差不多的物体。质量更小速度更快也可以成立,但是你可以很容易想象,任何这样完全摧毁两个物体的碰撞会让地球几乎什么都不剩地飞向太阳。

相关知识延伸阅读
小行星为微型行星的一种。以太阳系而言,小行星属于太阳系小天体(SSSB),和行星一样环绕太阳运动,但体积和质量比行星小得多。广义的小行星大小介于流星体和矮行星之间,直径可从数米至1,000公里不等,包括在这个尺寸下太阳系里非彗星的所有小天体。

图解:盖斯普拉是第一个被拍摄到特写镜头的小行星。
但大部分的小行星都分布于内太阳系,加上外太阳系小天体(如半人马群和海王星外天体)的物理特性和内太阳系小天体有所差异,因此“小行星”一词更常被用于专指内太阳系非彗星的小天体。
参考资料
1.Wikipedia百科全书
2.天文学名词
3. Paul Walorski-physlink- Mike Assad-络厦零
如有相关内容侵权,请于三十日以内联系作者删除
转载还请取得授权,并注意保持完整性和注明出处
,




