考点十二:圆
一、知识点汇总
知识点一:圆的有关概念

知识点二:垂径定理及推论(直径与弦、弧之间的关系)
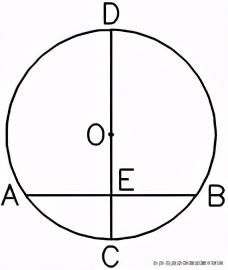
1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
2.推论一:平分弦的直径垂直于弦,并且平分弦所对的两条弧。
3.推论二:圆的两条平行弦所夹的弧相等。
知识点三:圆心角与弧、弦之间的关系
1.圆心角:顶点在圆心的角叫做圆心角。
2.圆心角与弧、弦之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;
(2)在同圆或等圆中,如果两个圆心角、两个弧,两条弦中有一组量相等,那么它们多对的其余各组量都分别相等。
知识点四:圆周角定理
1.圆周角:顶点在圆上,相等的圆周角所对的弧相等;
2.圆周角定理:在同圆或等圆中同弧或等弧所对的圆周角相等,都等于这条弧所对圆心角的一半;
3.推论一:在同圆或等圆中,相等的圆周角所对的弧相等;
4.推论二:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。

知识点五:圆的内接多边形

结论:(1)圆内接四边形对角互补.
(2)若凸四边形对角互补,则四个顶点共圆.
知识点六:切线判定
1.切线的性质:圆的切线垂直于过切点的半径。
2.切线的判定:
(1)和圆只有一个公共点的直线是圆的切线;
(2)如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线;
(无交点、作垂线、证相等)
(3)经过半径的外端,并且垂直于这条半径的直线是圆的切线。(有交点、连半径、作垂直)
知识点七:附加圆内模型
模型一: 切线长定理

结论:1从圆外一点向圆引两条切线;2AB=AC.
模型二:弦切角定理

结论:1弦切角等于它所夹的弧所对的圆周角;
2两个弦切角所夹的弧相等,那么这两个弦切角也相等.
模型三:相交弦定理

结论:.

模型四:切割线定理

结论:.

模型五:割线定理

结论:.

模型六:内切圆和外接圆
(1)内切圆


(2)外接圆


模型七:四心
1.重心:中线交点;
2.垂心:高线交点;
3.内心:角分线交点,内切圆圆心;
4.外心:垂直平分线,外接圆圆心。
知识点八:弧长及扇形面积计算







