切平面方程怎么求（平面的正交方程）

在几何学中，术语“法线”定义了一个物体，比如垂直于给定物体的向量或直线。 在这里，你会看到平面的正交方程。 如果有两个条件是已知的，这就可以确定。 一个是垂直于平面的另一个是平面到原点的距离。 在本文中，您将学习平面的矢量方程以及笛卡尔形式。

平面的法向表达和直角坐标表达

平面的正交的表达方程是：

其中→r是平面上一点的位置向量，n^是沿连接原点和平面的法向量的单位法向量，d是平面到原点的垂直距离。

设P (x, y, z)是平面上的任意点，O是原点。 然后,我们有,

n^的方向坐标是 (l ,m ,n)， 所以有：

由方程r. n = d，我们得到

因此，平面方程的标准形式的直角坐标形式为:

正交方程形式的平面例子

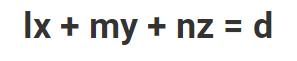
例 1:

一个平面与原点的距离为9/√38 。从原点起它的法向向量为：

5i^ 3j^ – 2k^.

求平面的向量方程式。

解:

令法相矢量为:

现在求出法向矢量的单位矢量：

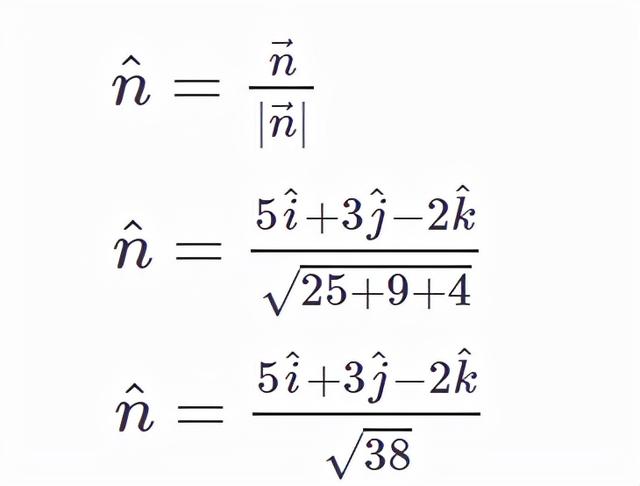
因此，将其代入向量方程即可得到所需的平面方程的向量表达为:

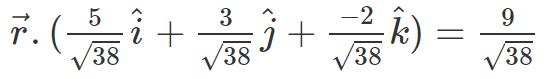
例2:

求出下列平面的直角坐标方程：

解:

因为r是平面上的一个点，用直角坐标替换（1）有：

所以直角坐标平面方程为 x y – z = 2.

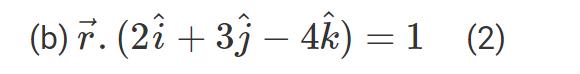
我们知道对于平面上任意点P(x, y, z)位置向量为:

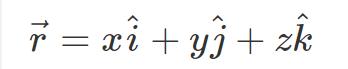
带入（2）式：

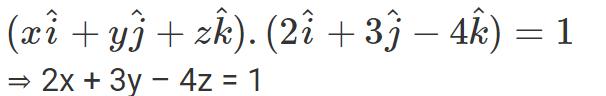
所以直角平面的坐标方程为 2x 3y – 4z = 1.

,