谁算的地球多重（是谁用什么秤把它称出来的呢）

现在科学界的认识是，地球质量为5.965x10^24kg，也就是约60万亿亿吨。在这里我们首先要弄清楚质量和重量的区别。

地球是没有重量的，或者说地球在不同的环境下，重量是不一样的。

重量是物体受重力大小的度量，也就是引力导致的度量。同样质量的东西，重力越大的地方就越重，重力小的地方就越轻。

比如一个人在地球上有60公斤重，到了月球，重力只有地球的六分之一，用秤一称，就只有10公斤。

地球在太空中属于失重状态，没有重量，而到了一个重力巨大的星球上，重量就会增加。

事实上重量的单位不是克或公斤，那是质量单位，重量单位是牛顿，符号为N。

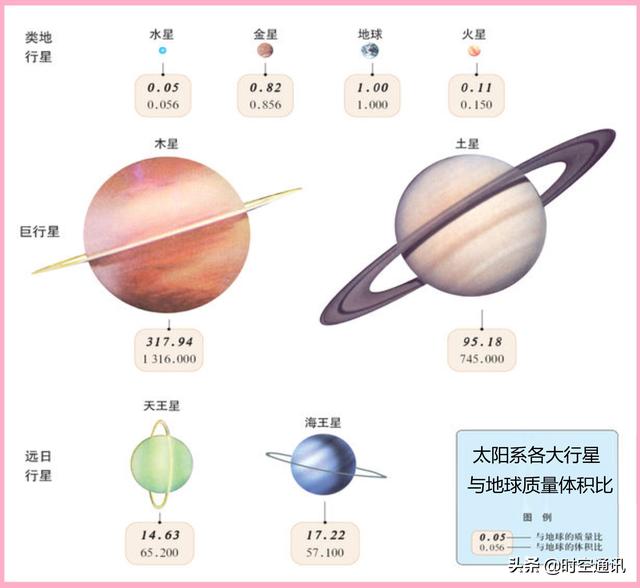
重量是物体受万有引力作用后的度量，在地球引力下，重量和质量是等值的，1公斤物质产生的重量为9.8牛顿（N）。

1公斤质量的物质，在太阳系不同的星球上重量为：水星3.76N、金星9.03N、地球9.81N、火星3.8N、木星23.4N、土星11.6N、天王星11.5N、海王星11.9N、月球1.62N。

而质量是物体具有的一种物理属性，是物质量的量度，是一个正的标量。

质量的根本属性是惯性，物体的惯性与质量成正比，质量越大的物体惯性越大，需要改变物体运动姿态的力越大。

质量是量的量度，因此质量的量在任何重力条件下都是一样的，在不同的星球上，物质重量改变但质量不变，因为称取质量的度量衡为天平，一千克的棉花和一千克的黄金在质量上是等价的，在不同的重力条件下天平的两边都是平衡的的。

所以地球质量在怎样的重力条件下都是一样的，为约60万亿亿吨。

这个世界又没有那么大的天平，能够把地球放进去称。那么这个60万亿亿吨质量又是怎样得来的呢？

这就是科学理论的威力。

古时候有曹冲称象，没有那么大的秤，曹冲就把大象赶上船，在船上刻下吃水的深度，然后把大象牵下来，装上石头，到同样的吃水深度，然后分多次称出石头的重量，大象的重量就出来了。

曹冲聪明，科学家比他还聪明。这位首次“称出”地球质量的人叫卡文迪许。

卡文迪许当然也没有那么大的秤来称地球，即便有，也无法称出地球的重量。他也是利用科学的知识，经过精密的测量和计算，坚持不懈几十年，终于得出地球质量的。

根据牛顿万有引力定律，引力大小与物体的质量成正比，与距离平凡成反比，这样我们就可以得出公式：F=GMm/r^2

其中F为引力量，G为引力常数，M和m为引力相互作用的大小物质分别质量值，r为物体的半径。

根据这个公式，人们知道了引力相互作用的两个天体的质量。通过与引力常数的乘积与半径平方之商，就能够计算出某个天体的引力值，通过反算，知道了某个天体的引力值，也就知道了天体的质量。

但要精确计算出地球质量，必须先有精确的引力常量G，那个时代还没有谁给出这个常量。

因此卡文迪许究其半生进行了获取这个数据的精密实验，这个实验使用的方法就是著名的扭秤实验。

他在一根长6英尺（约合1.83米）的木棒两头，固定住两个小金属球，形成一个哑铃样杠杆，中间用金属线悬吊起来，再将两个350磅的铜球放在小金属球附近，然后观察引力对它们的影响。

引力是世界上最弱的力，这么微小的金属球引力当然非常微弱，一般是很难观测到它们引力相互作用的。

但聪明的卡文迪许用镜子反射法放大了这种效应，小金属球微弱的移动被镜子反射到很远的地方，放大了许多倍，这样就能清晰的看到其移动的刻度，从而卡文迪许计算出了引力常量：G=（6.754±0.041）×10N^-11·m^2/kg^2。这个值同现代值G=6.67259×10^¹¹N·m^2/kg^2相差微小。

在此基础上，卡文迪许计算出了地球的密度和质量，得到地球质量为5.977x10^24kg的结果，与现代精确值5.965x10^24千克基本吻合。

但一直到现在，科学界对于卡文迪许到底有没有测得引力常量还存在争议。

因为在科学的历史记载中，引力常量G在卡文迪许“测量地球密度的实验”（Experiments to determine the density of the earth）的论文中并没有出现，在卡文迪许在世的时代，也没有出现G的使用记载。

G作为引力常量，是在卡文迪许论文发表75年后的1873年，才在一篇论文中提到，这时卡文迪许已经逝世了六十多年。

引力常数G正式进入人们视野的时间还要延后，是一个叫伟农·波伊斯的人，在英国皇家学会提出了重力常数G，此后，这个准确的表述才为科学界所接受。

但卡文迪许的贡献是肯定的，后人根据他的实验结果整理出了G=3g/4pirp，实际上他的实验得出的结果与后人提出的引力常数基本一致。只不过卡文迪许那个年代的科学家们更关心密度，因此卡文迪许得出了地球密度为水的5.481倍，与现在精确数据5.508倍也是异常接近的。

实际上有了密度和地球半径，就能够计算出地球大致质量。

地球半径为6371千米，根据球体积计算公式V=4/3 πr^3，得出地球体积为1.0832073×10^12km³，而地球平均密度为5507.85kg/m³，地球体积乘以密度，就能够得出地球质量。

但地球密度分布并不均匀，因此计算质量还是有一定误差。后来人们就用引入引力常数和重力加速度，随着引力常数越来越精确，计算的地球质量也被就越来越精确了。

这个公式为：M=gR^2/G

M为地球质量，g为重力加速度，R为地球半径，G为引力常量。

目前中国科学家罗俊团队经过三十年努力，测得的G值是最高精度万有引力常数，但所采取的方法依然是卡文迪许的扭秤实验，不过现在已经繁琐复杂精密多了。

这次他们同时采取了扭秤周期法和扭秤角加速度反馈法等两种独立方法，增加了测量结果的可靠性，得到了国际最精度的G值，达到万分之一精度水平。

这样地球的质量评估将会越来越精准。

这就是地球质量的来历。

时空通讯专注于老百姓通俗的科学话题，欢迎一起讨论。感谢粉丝朋友们一直以来的关注支持和厚爱。

原创版权，未经作者许可的任何转载、内容引用都被视为侵权抄袭，可能受到法律责任追究，请理解合作，谢谢。

​

,