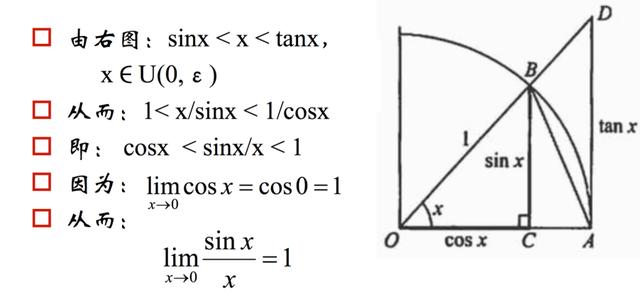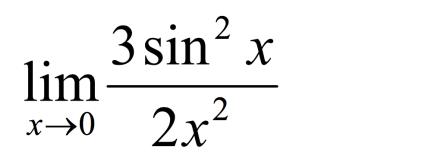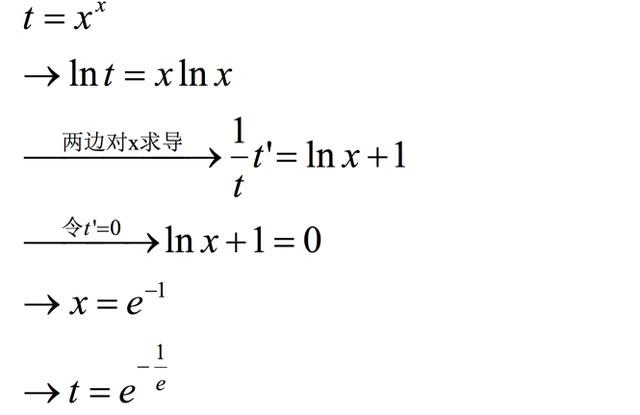本文为系列文章,内容高度总结为以下三大类:
机器学习背后的数学知识
常用的机器学习算法原理与示例
工程实践与应用案例/经验
每个大类中的内容很多,因此将分为多篇文章介绍给大家。本篇文章为第2篇,主要初步介绍高等数学相关知识。近期内容如下:
机器学习初步(第1篇)
1、概念定义
2、ML分类
3、算法一览
相关高等数学回顾(第2篇)
1、导数/梯度
2、Taylor展开
3、凸函数
相关概率论回顾(第3篇)
1、古典概率
2、贝叶斯公式
3、常见概率分布
高等数学回顾如果只是将机器学习当作一个黑盒使用的话,是可以不用学习这些数学知识的。
但如果你需要了解机器学习底层知识;需要对机器学习算法进行调优;需要应聘机器学习算法工程师岗位的话,建议大家还是要学习以下高等数学知识。
微积分之:两边夹定理/夹逼定理
推论:
该式将三角函数和多项式建立了极限关系
思考
该式的极限是多少?
导数
简单的说,导数就是曲线的斜率,是曲线变化快慢的反应。
二阶导数是斜率变化快慢的反应,表征曲线的凹凸性。
在GIS中,往往一条二阶导数连续的曲线,我们称之为光顺的。
还记得高中物理老师时常念叨的吗?加速度的方向总是指向轨迹曲线凹的一侧。
常用函数的导数
应用
已知函数
求f(x)的最小值?
领会幂指数的一般处理套路
在信息熵章节中将再次遇到它
求解
附:
在计算机算法跳跃表Skip List的分析中,用到了该常数。
背景:跳表是支持增删改查的动态数据结构,能够达到与平衡二叉树,红黑树近似的效率,而代码实现简单。
Taylor公式——Maclaurin公式
Taylor公式的应用1
数值计算:初等函数值的计算(在原点展开)
在实践中,往往需要做一定程度的变换
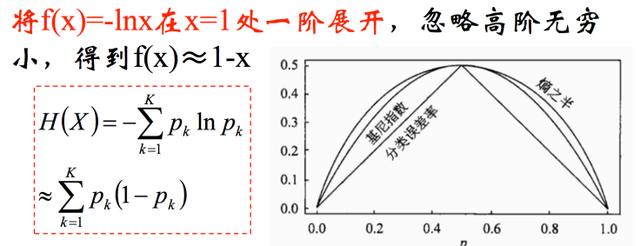
Taylor公式的应用2
考察基尼指数的图像、熵、分类误差率三者之间的关系
上述结论,在决策树章节中会进一步讨论
方向导数
梯度
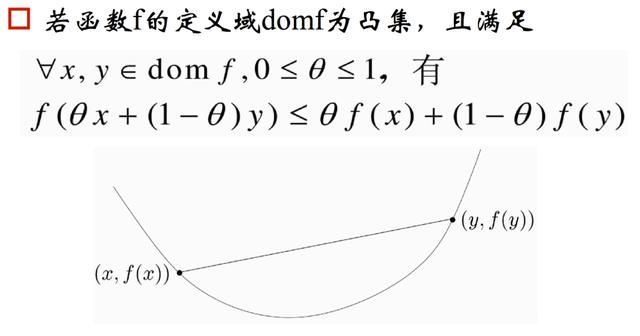
凸函数
凸函数的判定
即:一元二阶可微的函数在区间上是凸的,当且仅当它的二阶导数是非负的。
凸函数的表述
意义:可以在确定函数的凹凸性之后,对函数进行不等式替换
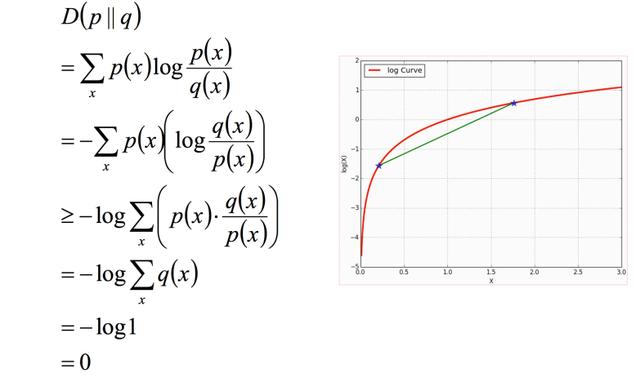
凸性质的应用
上式在最大熵模型等内容中会详细讨论。
注意到y=-logx在定义域上是凸函数
目录介绍
本系列文章所有内容计划如下:
机器学习与相关数学初步
数理统计与参数估计
矩阵分析与应用
凸优化初步
回归分析与工程应用
特征工程
工作流程与模型调优
最大熵模型与EM算法
推荐系统与应用
聚类算法与应用
决策树随机森林和adaboost
SVM
贝叶斯方法
主题模型
贝叶斯推理采样与变分
人工神经网络
卷积神经网络
循环神经网络与LSTM
Caffe&Tensor Flow&MxNet 简介
贝叶斯网络和HMM
词嵌入word embedding
本文就先介绍到这,大家有什么需求,欢迎给我留言。
,