
走马灯数
一、走马灯数142857在六九神神中,142857被称为数金数{见神奇的六九神数(一)};神金数又被称为走马灯数;这是世界上最著名的几个数之一 ,也许很多人很小的时候,就会在趣味数学里看到这个数。而这个神秘的数,最早发现于埃及的金字塔内。
(一)走马灯数的升序排列:
为什么说142857是 走马灯数 呢?
这是因为,它 的2~6 倍,都恰好是这六个数字的重新排列,而且是从小到大的升序排列:
142857=1*142857
285714=2*142857
428751=3*142857
571428=4*142857
714285=5*142857
857142=6*142857
(二)六组走马灯数的142857排列
把2~6倍神金数的升序排列换成开头数字分别为1,4,2,8,5,7的六组神金数:
142857=1*142857
428751=3*142857
285714=2*142857
857142=6*142857
571428=4*142857
714285=5*142857
这六组数字也正好是142857的重新有序排列,也具有走马灯数的特征;可以把这六组数字做成“神金数马灯图”;
(三)神金数马灯图

神金数马灯图
神金数马灯图说明:
① 图右边是开头数字为1,4,2,8,5,7的六组走马灯数Mn
Mn = n A
A=142857
n=1,3,2,6,4,5
M1=1A=1*142857=142857
M3=3A=3*142857=425871
M2=2A=2*142758=285714
M6=6A=6*142875=857142 M4=4A=4*142857=571428
M5=5A=5*142857=714285
② 走马灯数是从下到上竖立排列,从M1开始从左到右按照步数走动:
M1→M3→M2→M6→M4→M5→ ... ...
142857→428571→285714→857142→571428→714285→...
n=1→3→2→6→4→5→...
③ 图左边是“六字马灯钟”
马灯钟有两根针:头数针和尾数针;
马灯钟的两根针按照顺时针方向同时走动,每步走一个字;
头数针的走字顺序:1→4→2→8→5→7→从头开始...
尾数针的走字顺序:7→1→4→2→8→5→ 从头开始...
头数针和尾数针之间的六个数字是一组走马灯数;
头/尾数针的每一步对应右图的一组走马灯数;
始步M1→1步M4→2步M2→3步M8→4步M5→5步M7→ ...
142857→428571→285714→857142→571428→714285→...
六九神数家族中的走马灯数除了神金数142857之外,还有没有其它的走马灯数呢?下面我们来看一看佛木数076923/153846.
二、走马灯数076923(一)六组走马灯数的076923排列
把076923的1,10,9,12,3,4倍做成开头数字分别为0,7,6,9,2,3的六组佛木数:
076923=1*076923
769230=10*076923
692307=9*076923
923076=12*076923
230769=3*076923
307692=4*076923
这六组数字正好是076923的重新有序排列,具有走马灯数的特征;和神金数142857一样,可做成“佛木数马灯图”;
(二)佛木数马灯图

佛木数马灯图
佛木数马灯图说明:
① 图右边是开头数字分别为0,7,6,9,2,3的六组走马灯数Mn
Mn = n A
A=076923
n=1,10,9,12,3,4
M1=1A=1*076923=076923
M10=10A=10*76923=769230
M9=9A=9*076923=692307
M12=12A=12*76923=923076
M3=3A=3*076923=230769
M4=4A=4*076923=307692
② 走马灯数是从下到上竖立排列;从M1开始从左到右按照步数走动:
M1→M10→M9→M12→M3→M4→ ... ...
076923→769230→692307→923076→230769→307692→...
n=1→10→9→12→3→4→...
③ 图左边是“六字马灯钟”
马灯钟有两根针:头数针和尾数针;
马灯钟的两根针按照顺时针方向同时走动,每步走一个字;
头数针的走字顺序:0→7→6→9→2→3→从头开始...
尾数针的走字顺序:3→0→7→6→9→2→ 从头开始...
头数针和尾数针之间的六个数字对应一组走马灯数;
头/尾数针的每一步对应右图的一组走马灯数;
始步M1→1步M10→2步M9→3步M12→4步M3→5步M4→...
076923→769230→692307→923076→230769→307692→...
三、走马灯数153846(一)六组走马灯数的153846排列
把076923的2,7,5,11,6,8倍做成开头数字分别为1,5,3,8,4,6的六组佛木数:
153846=2*076923
538461=7*076923
384615=5*076923
846153=11*76923
461538=6*076923
615384=8*076923
这六组数字正好是153846的重新有序排列,具有走马灯数的特征;和佛木数076923一样,也可以做成“佛木数马灯图”;
(二)佛木数153846马灯图
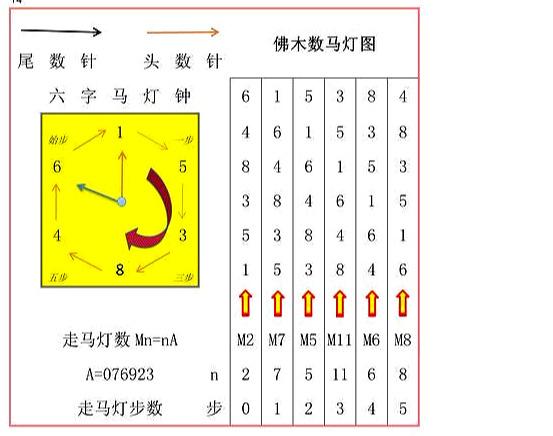
佛木数153846马灯图说明:
① 图右边是开头数字分别是1,5,3,8,4,6的六组走马灯数Mn
Mn = n A
A=076923
n=2,7,5,11,6,8;
M2=2A=2*076923=153846
M7=7A=7*076923=538461
M5=5A=5*076923=384615
M11=11A=11*76923=846153
M6=6A=6*076923=461538
M8=8A=8*076923=615384
② 走马灯数字是从下到上竖立排列,从M2开始从左到右按照步数走动:
M2→M7→M5→M11→M6→M8→ ... ...
153846→538461→384615→846153→461538→615384→...
n=2→7→5→11→6→8→...
③ 图左边是“六字马灯钟”
马灯钟有两根针:头数针和尾数针;
马灯钟的两根针按照顺时针方向同时走动,每步走一个字;
头数针的走字顺序:1→5→3→8→4→6→从头开始...
尾数针的走字顺序:6→1→5→3→8→4→ 从头开始...
头数针和尾数针之间的六数字对应一组走马灯数;
头/尾数针的每一步对应右图的一组走马灯数;
始步M2→1步M7→2步M5→3步M11→4步M6→5步M8→...
153846→538461→384615→846153→461538→615384→...
四、六九神数回顾走马灯数142857和076923的根分别为7,13(见杂交六九神数);根和神数相乘分别为7*142857=13*76923=999999;
把根和神数乘积=999999的神数称为六九神数。
(一)六九的因子分解
999999 = 3*3*3*7*11*13*37;
这7个因子中,任何一个因子或者它与其它因子的乘积都可以成为一个六九神数的根。这个根的倒数是一个无限循环小数。取小数点后面六位数的循环节就是我们要寻找的六九神数。把根除外的剩余因子的乘积,或用这个根去除999999就可以得到要寻找的六九神数。
(二)六九家族神数的素数根和合数根
素数根只有5个:3, 7, 11, 13, ,37。
合数根有:9,21,27,33,39,63,77,91, ... ...
(三)杂交神数和父母神数
合数根是2个以上素数的乘积;这些合数根被称为为杂交根,因为它是由两个以上素数杂交(相乘)而成;
和素数根对应的神数被称为父神数,和另外一个素数根对应的神数被称为母神数;和杂交根对应的神数被称为杂交神数,或者子神数;
和父/母神数对应的根被称为父/母根,和子(杂交)神数对应的根被称为子(杂交)根。
(四)走马灯数的子(杂交)神数
父神数142857/母神数076923
父根7/母根13
杂交根 7*13=91
1/91=0.010989010989...(无限循环小数)
取小数点后面六位数(第一循环节)010989,这就是我们要找的杂交(子)神数。
子(杂交)神数=010989
五、走马灯数的神奇规律(一)父母神数、父母根与子神数的关系
1. (父神数 母神数)÷ 子神数 = 父根 母根
(142857 076923)÷ 010989=20=7 13
2. (父神数-母神数)÷ 子神数 = 母根-父根
(142857-076923)÷ 010989=6=13-7
3. (父神数平方 母神数平方)÷ 子神数平方
= 父根平方 母根平方
(142857平方 076923平方)÷ 010989平方
=13平方 7平方=169 49=218
4. (父神数平方 - 母神数平方)÷ 子神数平方
= 母根平方 - 父根平方
(142857平方-076923平方)÷ 010989平方
=13平方-7平方=169-49=120
(二)六九【999999】规律
1. 父神数×母神数÷杂交神数=999999
142857×076923÷010989
=999999
2. M前六位 M后六位
= 999999
M=142857平方×076923平方÷010989平方
=999998000001
999998 000001=999999
3. W的前面6位数 中间6位数的和=999999
W=142857立方×076923立方÷010989立方
=999997000002999999
999997 000002=999999
4. W的后面6位数=999999
5. 神数和根的乘积是999999
神金数142857*7=999999
佛木数076923*13=999999
6. 头周期头尾两个数之和以及中间两个数之和都是999999
① 头尾两个数之和=999999
神金数
头数1*142857
尾数6*142857=857142
头尾数两个数字之和
142857 857142=999999
佛木数
头数1*076923
尾数12*076921=923076
头尾数两个数字之和
076923 923076=999999
② 中间两个数之和=999999
神金数
第三项3*142857=428751
第四项 4*142857=571428
中间两个数之和
428751 571428=999999
佛木数
第六项6*076923=461538
第七项7*076923=538461
中间两个数之和
461538 538416=999999
(三)五九[99999]规律
1.M的前面5位数是99999
M=父神数平方×母神数平方÷子神数平方=999998000001
2.W的前面5位数是99999
W=父神数立方×母神数立方÷子神数立方=999997000002999999
(四)三九[999]规律:
1. 走马灯数头周期各项和它的倒顺序数都是999的倍数
这个倍数是:各项前面三位数字 1(999999项 2)
① 神金数m
a. 头周期神金数各项
m=142857n n=1,2,3...7
第1项142857/ 999 =143
第2项285714/999=286
第3项428571/999=429
第4项571428/999=572
第5项714285/999=715
第6项857142/999=858
第7项999999/999=1001
b. 它的倒顺序数:
第1项758241/999=759
第2项417582/999=418
第3项175824/999=176
第4项824175/999=176
第5项582417/999=583
第6项241758/999=242
第7项999999/999=1001
② 佛木数m
a. 头周期佛木数各项
m=76923n n=1,2,3...13
第1项076923/999=77
第2项153846/999=154
第3项230769/999=231
第4项307692/999=308
第5项384615/999=385
第6项461538/999=462
第7项538461/999=539
第8项615384/999=616
第9项692307/999=693
第10项786230/999=770
第11项846153/999=847
第12项923076/999=924
第13项999999/999=1001
b. 它的倒顺序数:
第1项329670/999=330
第2项648351/999=649
第3项967032/999=968
第4项296703/999=297
第5项516483/999=517
第6项835164/999=836
第7项164835/999=165
第8项483516/999=484
第9项703296/999=704
第10项032967/999=33
第11项351648/999=352
第12项670329/999=671
第13项999999/999=1001
2. 神数前面三位数 后面三位数之和是999
神金数 142857 148 857=999
佛木数 076923 076 923=999
****** 153846 153 846=999
(五)二九[99]规律:
1. 走马灯数头周期各项和它的倒顺序数都是99的倍数
① 神金数
a. 头周期神金数各项
m=142857n, n=1,2,3, ...7
第1项142857/99=1443
第2项285714/99=2886
第n项/99=1443n
第7项999999/99=10101
b. 它的倒顺序数
第1项758241/99=7659
第2项417582/99=4218
... ... ...
第7项999999/99=10101
② 佛木数076923
a. 头周期佛木数各项
m=076923n n=1,2,3, ...13
第1项076923/99=777
第2项153846/99=1554
... ... ...
第n项/99=777n
第13项999999/99=10101
b. 它的倒顺序数
第1项329670/99=3330
第2项648351/99=6549
... ... ...
第13999999/99=10101
2. 三个两位数字之和是 99
神金数 142857 14 28 57=99
佛木数 076923 07 69 23=99
******* 153846 15 38 46=99
(六)一九 [9] 规律:
1.走马灯数头周期各项和它的倒顺序数都是都是9的倍数。
③ 神金数
c. 头周期神金数各项
m=142857n, n=1,2,3, ...7
第1项142857/9=15873
第2项285714/9=31746
第n项/9=15873n
第7项999999/9=111111
d. 它的倒顺序数
第1项758241/9=84269
第2项417582/9=46398
... ... ...
第7项999999/9=111111
④ 佛木数076923
c. 头周期佛木数各项
m=076923n n=1,2,3, ...13
第1项076923/9=8547
第2项153846/9=17094
... ... ...
第n项/99=8547n
第13项999999/9=111111
d. 它的倒顺序数
第1项329670/9=36630
第2项648351/9=72039
... ... ...
第13999999/9=111111
2.各位数字之和是9的倍数
1 4 2 8 5 7=27=3*9
0 7 6 9 2 3=27=3*9
3.六位数字的不同排列也是9的倍数
1) 神金数142857
① 这6个数字的任排列都是9的倍数。
N取M的排列=N!/(N-M)!
6取6的排列= 6!/(6-6)! =6!/0!=6! (0!=1)
6取6的排列= 6!= 1*2*3*4*5*6=720都是9的倍数。
② 包括7个神金数本身:
142857,285714,428571,571428,857142,999999.
③ 以及它的7个倒顺序数:
758241,417582,175824,824175,241758,999999.
2) 佛木数076923
这6个数字取6的排列=720都是9的倍数。
包5个佛木数本身:
076923,230768,307692,692307,923076;
以及它的5个倒顺序数:
329670,867032,296703,703296,670329.
3) 佛木数153846=2*076923
这6取6数字的排列=720都是9的倍数。
包括5个佛木数本身:
153846,384615,463518,538461,846153;
以及它的5个倒顺序数:
648351,516484,815364,164835,351648.
两个佛木数(076923/153846)的排列共有720 720=1440 个数,都是9的倍数。
六、 其它走马灯数除了142857,076923,153846之外,还有很多其它走马灯数,但是,它们不在
六 九神数的范围之内;以后有机会再聊!希望有兴趣的朋友关注。
,




