上一节中介绍了函数与数列的相似之处,而收敛数列与函数极限的性质也有许多类似的地方,下面我们以函数极限的性质为例来探讨收敛数列与函数极限的性质。
(3)收敛数列与函数极限的性质
首先我们要引入单侧极限的概念:
函数极限定义中的自变量X趋近于某个常数,X可以从左侧趋近,当然也可以从右侧趋近。
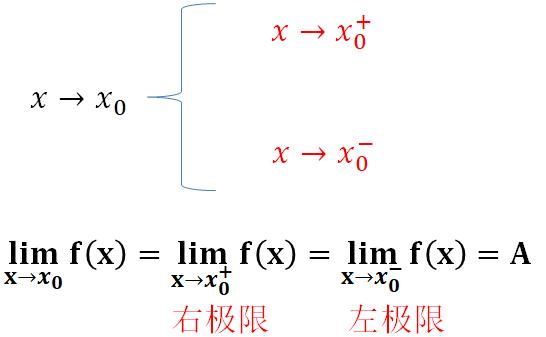
下面我们就来证明这个定理:

来看函数f(x)的图像,我们可以发现:
当自变量X趋近0的左侧时,函数的值趋近于负无穷。
当自变量X趋近0的右侧时,函数的值趋近于正无穷。
显然函数在X趋近于0的左右极限不唯一,那么我们能认为函数的极限可以不唯一吗?
用反证法:

首先, x→a本来就是一个局部的概念,表示X位于a附近的一个去心领域内,
举个简单的例子,如f(x)=x, 显然这个函数在x趋近于1时的极限值就是1,也因此函数在点x=1处一个很小的去心领域内是有界的,如区间(0.9999,1)∪(1,1.00001)内显然是有界的。

还是以f(x)=x为例,x趋近于1时的极限值是大于0的,显然在存在一个在x=1附近的领域如(1,100001)内函数的值大于0.

最后与函数极限的性质比较,可得收敛数列的一些相应性质:
定理1 (极限的唯唯一性) 如果数列{Xn}收敛,那么它的极限唯一定理2 (收敛数列的有界性) 如果数列{Xn}收敛,那么数列{Xn}一定有界定理3 (收敛数列的保号性) 如果数列{Xn}的极限值为A,且当A>0(或A<0),那么存在正整数N,当n>N时,都有Xn>0(或Xn<0)谢谢观看
限于作者水平,若有不妥之处望广大读者指正,共同进步。
,




