
U ⊆ C是一个全纯函数, γ : [a; b] U是平滑的闭合曲线。如果γ是同伦的常数曲线,那么我们有
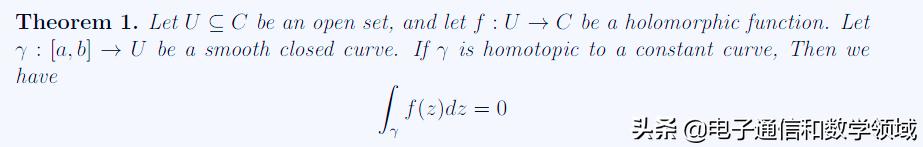
让f(z) = log(1 z)=z。利用柯西积分定理,我们可以这样写

然后我们可以根据方程(2.5)和(2.6)写出

参数化CC3 as -1 e^it : 0 ≥ t ≥ t0, 对于某些t0,我们得到

这两个积分都有上界,因为我们通过ML不等式知道

第一个积分乘以 log(),它们都趋近于0。因此积分log(1 z z)dz也趋近于0。还要注意,C1趋向于完整的外圆

请注意,进一步我们得到

这就得出I = 0的结论。由(2.7)和(2.8)得到,利用(2.3)和式(2.2),我们得出结论






