著名的开普勒猜想提出三维球体(大小相同)的最密堆积百分数为
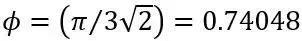
。在这种堆积方式中,上一层小球落在下一层小球空隙的中心,以球心位置为晶格格点形成的点阵结构在晶体学中被称为面心立方(FCC)晶系,对应的最近邻配位数为12。这是硬球按照有序排列的结果,而对于更广泛存在的无序介质来说,如何确定球体在无序组合中占据最密堆积百分数,即所谓的随机密堆积(random close packing, RCP)问题仍然是当代物理学和数学中一个开放的核心问题。显然,这个问题的解决对我们理解非晶态物质的本质与玻璃转变现象至关重要。

针对这个问题,米兰大学的Alessio Zaccone教授给出了二维、三维情况下随机密堆积体积分数的显示解析解,其中三维的结果为ϕ=0.65896,二维的结果为ϕ=0.88648。相关论文以“Explicit Analytical Solution for Random Close Racking in d =2 and d = 3”为题,发表在物理学顶级期刊Physical Review Letters上并选入编辑推荐,Alessio Zaccone教授为论文的唯一作者。
论文链接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.028002

论文首先综述了随机密堆积问题的研究现状,指出最密堆积百分数的唯一确定至少受到来自两个方面的阻碍。其一是ϕRCP显著依赖于堆积的形式,由于广泛存在的堆积形式,ϕRCP在已有的报道工作中展现出较为宽泛的取值区间,三维下为ϕRCP=0.60-0.69,二维下为ϕRCP=0.81-0.89。其二是对“随机堆积”的准确定义,不同的定义必然导致不同的搜索区间,进而得到的ϕRCP也会存在一定差异。
随后,针对这些难点,论文提出了一个形式简单的解析理论来准确预测二维和三维情况下的ϕRCP。首先依据力学稳定性给出随机密堆积状态的准确定义,即随机密堆积状态正好使得粒子相互作用可以平衡掉系统非仿射弛豫带来的能量耗散。当堆积状态趋于更紧密时,系统是刚性的,处于阻塞状态(jammed)。当堆积状态更松软时,系统不是刚性的,具有承担进一步非仿射重排的潜力,进而寻找更致密的堆积状态。因此,随机密堆积状态对应的是力学刚性的起始,即有限剪切模量涌现时的状态。进一步,作者应用修正的液体状态理论,基于径向分布函数的概念,给出局部配位数的表达式。进一步可以得到约化的接触区概率密度函数,根据硬球液体的概率统计理论以及Percus-Yevick理论给出在给定区域内找到粒子的概率的解析表达式。最后结合随机密堆积状态的定义,可以推导出对应的体积百分数的显示解析表达式。作者给出了二维,三维随机密堆积的结果,即二维随机密堆积百分数为ϕRCP=0.886848,三维随机密堆积百分数为ϕRCP=0.65896。这个结果处于现有文献报道的随机密堆积百分数取值区间内。
最后,作者指出这个理论框架具有进一步拓展的科学价值。(1)其可以拓展到研究非球体的粒子的随机密堆问题。(2)目前的结果是针对常见的二维,三维情况,但是这个理论可以进一步推广至更高维度的空间。通过适当的修正模型表达式和参数可以预测高维空间的随机最密堆积情况,从而得到显示的ϕRCP-d(d是维度)关系。(3)将本文的理论框架应用于存在固有接触网络的系统中,如自由连接的硬球链或者线性聚合物球链等的阻塞(jamming)问题中,可能获得对玻璃转变问题的新理解。
研究工作对深入理解非晶材料提供了有效的工具和广阔的视角。
*感谢论文作者团队对本文的大力支持。
本文来自微信公众号“材料科学与工程”。欢迎转载请联系,未经许可谢绝转载至其他网站。
,




