德摩根定律指出,两个集合的并集的补集是它们的补集的交集, 这是数学家摩根提出的。 该定律可以表示为(A∪B) ' = A '∩B '。 在集合理论中,这些个定律用补集将集合的交集和并集联系在一起。

德摩根定律的陈述和证明
将定义良好的对象或元素称为集合。 可以在两个集合上执行集合的补、并和交等各种运算。 这些操作和它们的使用可以进一步简化,使用德摩根定律可使这些操作和使用一步简化 。
任何由与特定上下文相关的所有对象或元素组成的集合都被定义为全集。 考虑一个全集U,使A和B是这个全集的子集。
根据德摩根第一定律,两个集合A和B的并集的补集等于集合A和B的补集的交集。
(A∪B) ' = A '∩B '——(1)
其中集合的补集定义为:
A’= {x:x ∈ U and x ∉ A}
其中A '表示A的补集。
这个定律可以很容易地用维恩图来表示。
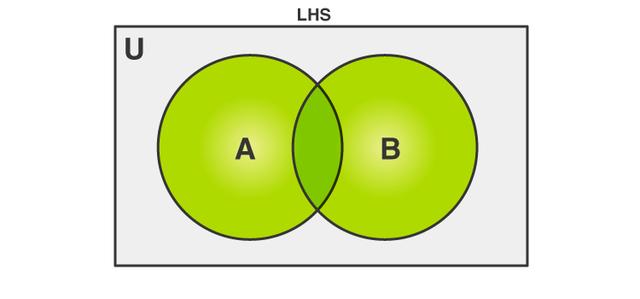
突出显示的绿色部分表示A∪B。 A与B的并集的补集即(A∪B) '是所有不在A∪B内的元素的集合。 这可以如下图所示:

同样,方程1的右侧也可以用维恩图表示,第一部分即A '可以表示为:

黑色部分表示集合A,蓝色部分表示补集A '。
类似地,B '表示为:

黑色部分表示集合B,黄色部分表示其补集,即B '。
如果将图3和图4相互叠加,得到的图与集的补集相同。

因此,左侧 = 右侧
数学上根据集合的含义推理,
A∪B=在A中或在B中
(A∪B) ' = 左侧 = 即不在A也不B中
A ' = 不在A中
B ' = 不在B中
A '∩B ' =不在A也不在B
⇒(A∪B)’= A’∩ B’
因此,通过可视化的维恩图和分析德摩根定律,将其写下来,它的有效性可以被证明。
个定理也被用来解决布尔代数中的不同问题。
,




