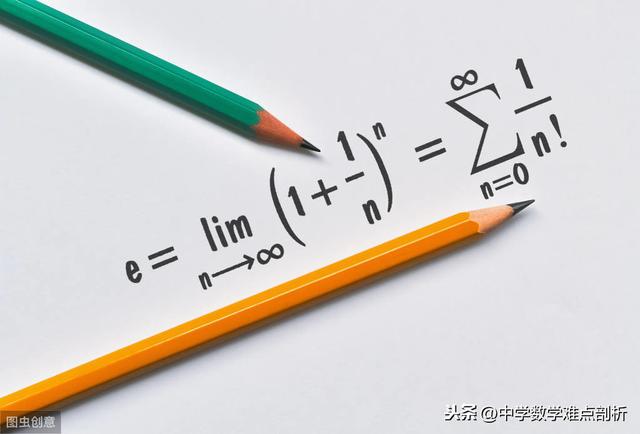生活中的数学
似乎许多人不喜欢数学。许多学生常常会问这样抱怨:“我为什么要学这些东西?平时又用不上。”但事实上,作为一个成年人,了解一些基本的数学概念对日常生活是至关重要的。我们在清点现金时,计算房贷时,填写纳税申报表时,都需要数学。事实上,许多金融事务在过去都促进了数学本身的发展。例如,负数最初主要是用来代表债务的。

生活中,我们还经常提到指数增长这个数学概念。指数增长其实指的是这样一种增长:一个系统在一段时间之后会数量翻倍。当然,数量可以翻两倍,翻三倍,翻n倍。指数增长的一个例子就是细菌的繁殖问题。如果培养皿中细菌每隔一段时间数量翻倍,并且繁殖没有任何限制条件的话,那么它们的数量会指数增长下去。
指数增长的另一个熟悉的例子是摩尔定律——一个由英特尔创始人之一戈登·摩尔的名字命名的规律。1965年,摩尔注意到,晶体管的体积迅速减少,这意味着电脑芯片可以装下更多的晶体管,于是他预测,芯片的处理能力大约每两年就会翻一番。这种指数增长已经持续了几十年了,但许多人认为随着技术的限制,摩尔定律过不多久就会失效。
e的魔力
现在,我们来假设有一家银行的年利率是100%。如果计算利息的周期(计息期)是1年的话,那么到了年底,100元就会变为200元。如果你幸运地找到这家银行并存了些钱的话,那么你的钱就会指数增长下去。
如果计息期变短了,你就会获得更多的利息。比如,那家银行的计息期是半年的话,那么6个月之后,会有50元算入本金中,然后在此基础上计算下一期的利息。这样,到了年底时,除了原来的本金产生的100元利息以外,还有50元经过半年产生的利息,为25元。这样,最终银行返还客户的本息为225元,而不是200元。
如果计息期是一个季度的话,那么前面季度的利息又可产生利息,年底最终的本息为244年。很显然,计息期越短,最终的本息就越多。但随着你把计息的时间缩得越来越短,那么增加的利息会越来越少。如果计息期是1天的话,那么最终的本息将是271元。也就是说,最终的本息是原来本金的2.71倍。
于是,就有了一个问题:如果利息每一分钟、每一秒钟,甚至更短的时间都计算在内,最终的本息是原来的多少倍呢?过去,数学家们一直没搞清楚这个问题,直到17世纪才搞清楚。1683年,瑞士数学家雅各布·贝努利找到了答案:2.7182818……这个数与π类似,是一个无理数。数学家们把这个数称为自然常数,并用字母e来代表它。
这种分分秒秒都把利息算在内的增长模式,被称为连续型复合增长,只要是这种增长模式,e便会出现。数学家们还发现,e是数学中最为基本的一个常数。现在,会计学、物理学、工程学、统计和概率论等许多学科中,都有它的身影。
找到真爱
关于e的应用,最有趣的例子就是秘书问题。想象有100个人应聘一份秘书工作,他们按照随机顺序接受面试,而面试官每次面试一人,面试过后便要立刻决定是否聘用他。如果当时决定不聘他,就不能再聘用他;如果聘用了他,整个面试立刻结束。如果面试官想把所有应聘者都面试一遍,那么这就相当于拒绝了前面99个申请人,不管最后一个申请人是否称职,都得录用。问题是,面试官何时做决定,才能以最大的机率得到最适合的人选?

数学家经过分析,认为最佳的办法是,先面试一部分人,然后在剩下的应聘者中,录取胜过或接近之前面试过的最好的应聘者。那么,应该先面试多少人呢?这个计算过程略复杂一些,答案就直接告诉你吧:100/e,约为37。就是说当你面试了37个人之后,选出其中最优秀的一位作为标准,在后面的应聘者遇到类似这样的人,就可以马上确定下来。事实上,这个例子也能适用于找对象。比如,如果你能有机会与100个人相亲,那么见了37个人之后,你就可以下决心与后面63个中的一位意中人谈谈恋爱。
所以说,数学知识不仅在算钱的时候有用,它有时候还会帮助你找到真爱。
,