2022国考推理分析技巧之拆分思路巧解截面图
近些年国家公务员考试行测中图形推理中有一类题目被广大考生诟病。因为自身空间想象力差,方法技巧性把握不到位,往往费时又错误率高,这类题目就是——截面图。截面图这类题目近些年成为国考中必考的一道题目,重点考察广大考生的空间想象能力。但是想象能力是“只可意会不可言传”,本篇文章就把截面图,这类题变成“即可意会,更能言传”!
在介绍截面图时,我们分为两步去思考问题。第一步,基础图形哪些能截出来,哪些不能截出来。第二步,复杂图形如何拆解成基础图形去解题。
我们先来看第一方面,常规图形的截面。
(1)立方体的截面
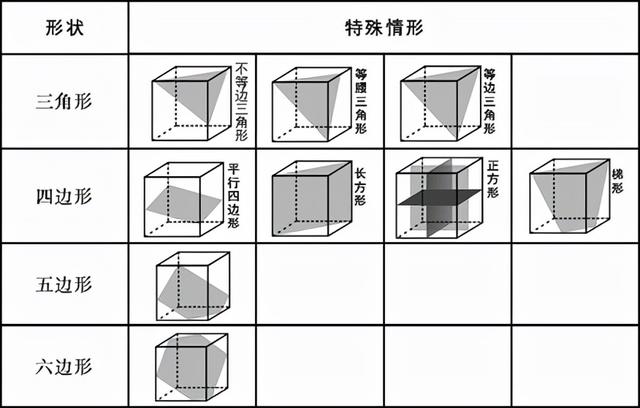
立方体可以截出:三角形、四边形、五边形、六边形。
立方体常见的考点:立方体无法截出直角三角形(也无法截出钝角三角形)。
(2)圆柱体的截面

圆柱体可以截出:矩形、圆、椭圆、半椭圆。
圆柱体常见的考点:圆柱体无法截出梯形。
(3)圆锥体的截面

圆锥体可以截出:圆、椭圆、抛物线、双曲线、三角形。
圆锥体常见的考点:圆锥截出椭圆时,椭圆应偏向一侧而非在正中间。
第二方面,将复杂图形拆解为基础图形。
一般我们在考试中很少会遇到单纯的基础图形,而往往是相对复杂的图形,这时我们需要有个“拆分思路”来看待图形,把相对复杂的图形,拆解成几个基础的图形,然后应用结论解题的过程。我们先看几个图形。
【图1】

图1不难看出,这个复杂图形是由一个立方体和内部挖空的圆锥体组成。所以拆分的基础图形为:立方体 圆锥体
【图2】

图2,是由外部一个大圆柱体和内部一个挖空的小圆柱体组成。所以拆分的基础图形为:大圆柱体 小圆柱体。
所谓复杂图形做拆分,就是一个把新问题,转换为基础性问题的过程。大多数题目都可以拆分为基础性的图形。当拆分为基础图形后,需要结合刚才的结论来解题。接下来我们用国考中的真题,来进一步了解拆分思路巧解截面图。
【例】(2020-国家)左图为给定的立体图形,将其从任一面剖开,以下哪个不可能是该立体图形的截面?


首先我们先观察左侧图形,先把复杂图形拆解成常规图形。左侧图形上半部分为一个立体的扇形图,下半部分为一个大一点的扇形图,这两个图形并不是我们刚才讲过的基础图形的截面。接下来我们再进一步思考,我们仔细观察图形下半部分,有些类似于刚才提到的圆柱体,只是区别在于本题图形是“缺了一块”的圆柱体。其实就可以近似看成圆柱体。接下来应用结论,圆柱体常见的考点:圆柱体无法截出梯形。换句话说选项中出现梯形形状的图形,理论上是无法截出的。此时观察选项,选项B下半部分为两个直角梯形,如图:因此根据结论,无法截出梯形,直角梯形更是无法截出,因此本题选无法截出的图形,答案为B项。
为了更好的让大家了解,我们把A项、C项、D项能截出的图形如下图所示。
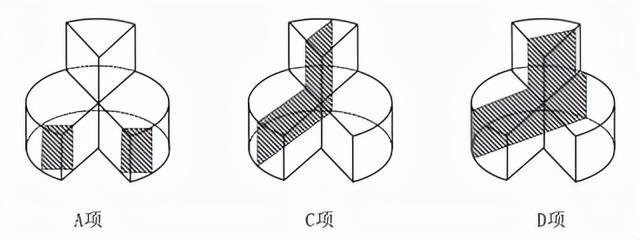
以上就是利用复杂图形拆分为基础图形,然后再利用结论做题过程,你学会了吗?