
图1
要理解梯度,必须先理解什么是方向导数。参照图1。z代表空间曲线。

图2 方向导数说明图
我们先看看方向导数的定义:

图二 方向导数的定义
所谓方向导数,就是指函数f(x,y)沿着直线L变化的速率,这条直线其实就是曲面上相对应的那条曲线在xoy平面的投影,完成投影的这个竖立的平面就称为投影平面,那么,方向导数其实就是空间曲线沿着它自己在xoy平面的投影直线的变化率。正如dy/dx表示二维平面中一条曲线在某一点沿着x轴的变化速率(也就是切线的斜率)一样,参考说明图,可以很清楚地理解方向导数的含义。有了定义以后,可以得出

图3
图3相当于把方向导数

在XOY平面进行了分解,然后再和一个单位向量做点积,这个单位向量就是

这里的角度

就是图2中xoy平面里面由P0点出发的不同的方向直线和x轴之间的夹角。当空间曲线 f 固定的时候,方向直线可以有无数条。那么,方向导数什么时候取得最大值呢?

由上面推论可知,方向导数就等于梯度和xoy平面中方向直线所指向的那个方向的点积。
注意,假设XOY平面有不同的方向直线,那么

梯度方向就是图2中的绿色投影平面在XOY平面截取的那根直线

显然,方向导数的最大值即梯度

图三
整个证明的思路就是先假设梯度的方向就是投影平面在图2中xoy平面中截取的直线L,梯度的方向就是图三,否则,梯度如果是别的方向的话,就会多出一个

因此得证。
下面解释梯度的含义。假设有如下的圆锥形曲面,这个曲面就是函数f(x,y),用一个平面去截取它,

之后得到如下的曲线

之后抬高平面,截取多根曲线后,将其投影到xoy平面,得到下图。

等高线图
可以看出,平面截取的f(x,y)=c,就是一根一根的等高线,其中c越大,说明高度越高,平面越在上面,从而截取的圆圈越小。图中的c1>c2。如果c是连续变化的,那么整个曲面就都投影到了xoy平面。那么,为什么说梯度的方向就是高度变化最快的方向呢?从图二方向导数的定义式可以看出,梯度是方向导数取到最大值的时候的数值,也就是比值取到最大值,那当然是高度变化最快的方向。那为什么梯度的方向就是等高线中该点的法线方向呢?注意,P点对应于圆锥曲面上的某一点。说明如下:

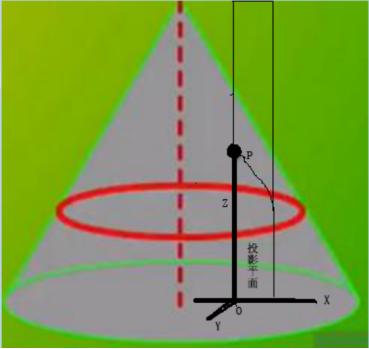
图4
最后,我们可以这样来理解梯度:梯度是为了解决帮助一个站在山坡(P点)的人,寻找一条到达山顶的最短路径(当然也可以到山坡的任何一点)这么一个问题。那么,怎么把等高线图和这个问题联系起来呢?为了解决这个问题,我们需要建立一个三维直角坐标系,其xoy平面就是山坡底部所在的平面,z轴就是P点所在的垂直于xoy平面的直线,即这个坐标系的原点就是山坡上P点在xoy平面的投影(图4)。当图2中的方向直线(包括投影平面)绕着原点转动时,必然在圆锥曲面(山坡)上会截取一条空间曲线,这条曲线就是站在山坡的此人沿着任意方向进行移动的轨迹。而当方向直线转到与等高线图中P点的法线方向一致的时候,就是方向直线找到了梯度的方向(注意,方向直线和梯度向量始终同时处于xoy平面内),而此时投影平面在山坡所截取的空间曲线,必然把此人站立的P点和山坡顶点连接起来,如果没有,那就不是梯度的方向,而且这条曲线就是此人通向山顶(不是山脚,山脚代表梯度的反方向)的最短路径。由此我们可以看出,梯度其实就是这条最短路径在山脚所在平面的投影。那么这个人沿着这条轨迹,每向山顶迈出一步,也就相当于在等高线图中,沿着梯度方向,从一条等高线跨越到了和它邻近的那条等高线。总之,梯度是一个向量,就是空间曲线由其投影平面在XOY平面所截取的那根直线,其值等于方向导数的最大值,方向就是该点在等高线图中的法线方向。
,




