电力基础
在开始探索电气和电子世界时,至关重要的是要了解电压,电流和电阻的基本知识。这是操纵和利用电力所需的三个基本组成部分。起初,这些概念可能很难理解,因为我们无法“看到”它们。人们无法用肉眼看到流过电线的能量或坐在桌子上的电池的电压。即使是天空中的闪电,尽管可见,但实际上并不是从云层到地球发生的能量交换,而是空气中对通过它的能量的反应。为了检测这种能量转移,我们必须使用万用表,频谱分析仪和示波器等测量工具来可视化系统中电荷的变化。但是不要害怕

电荷
电是电子的运动。电子产生电荷,我们可以利用电荷进行工作。您的灯泡,立体声音响,电话等都在利用电子的运动来完成工作。它们都使用相同的基本电源进行操作:电子的运动。
本教程的三个基本原理可以使用电子或更具体地讲,它们产生的电荷来解释:
- 电压是两点之间的电荷差。
- 电流是电荷流动的速率。
- 电阻是材料抵抗电荷(电流)流动的趋势。
因此,当我们谈论这些值时,我们实际上是在描述电荷的运动,从而描述电子的行为。电路是一个闭环,允许电荷从一个地方移动到另一个地方。电路中的组件使我们能够控制该电荷并使用它来工作。
乔治·欧姆(Georg Ohm)是一名巴伐利亚人的科学家,研究电力。欧姆首先描述由电流和电压定义的电阻单位。因此,让我们从电压开始,然后从那里开始。
电压
我们将电压定义为电路两点之间的势能量。一分比另一分多。两点之间的电荷差称为电压。它以伏特为单位进行测量,从技术上讲,这是两点之间的势能差,每经过一个电荷库仑,它将赋予一焦耳能量(如果没有意义,请不要慌张,所有这些都将予以解释)。单位“伏特”以意大利物理学家亚历山德罗·沃尔塔(Alessandro Volta)的名字命名,他发明了第一个化学电池。电压在方程式和示意图中以字母“ V”表示。
描述电压,电流和电阻时,常见的比喻是水箱。在这样的类比,电荷由水所表示的量,电压由水表示压力和电流通过水表示流量。因此,对于此类比喻,请记住:
- 水=费用
- 压力=电压
- 流量=当前
考虑一个比地面高一定高度的水箱。该水箱的底部有一个软管。
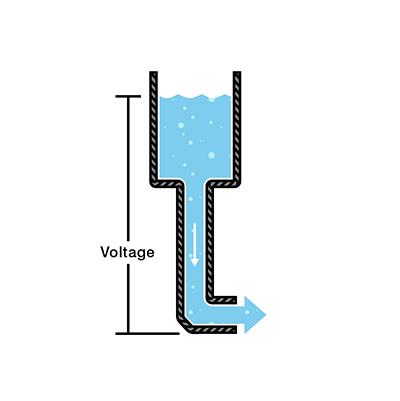
软管末端的压力可以表示电压。水箱中的水代表电荷。水箱中的水越多,充气量越高,在软管末端测得的压力就越大。
我们可以将这个储罐想象成一个电池,一个储存一定量能量然后释放它的地方。如果我们排空一定量的油箱,则在软管末端产生的压力会下降。我们可以认为这是电压的下降,例如当电池电量耗尽时手电筒变暗时。流经软管的水量也减少了。压力越小,意味着流动的水就越少,这将我们带入潮流。
当前
我们可以将水箱中流经软管的水量视为电流。压力越高,流量越高,反之亦然。用水,我们可以测量一定时间内流经软管的水量。利用电,我们可以测量一段时间内流经电路的电荷量。电流以安培为单位(通常简称为“安培”)。安培被定义为每秒6.241 * 10 ^ 18个电子(1库仑)通过电路中的一个点。安培在方程式中用字母“ I”表示。
现在说,我们有两个水箱,每个水箱底部都有一条软管。每个水箱的水量完全相同,但是一个水箱的软管比另一个水箱的软管窄。

我们在两个软管的末端都测量了相同的压力,但是当水开始流动时,软管较窄的水箱中的水流量将小于软管较窄的水箱中的水流量。较宽的软管。在电气方面,通过较细软管的电流小于通过较粗软管的电流。如果我们希望通过两个软管的流量相同,则必须使用较窄的软管增加水箱中的水量(充入量)。

这会增加较细软管末端的压力(电压),从而将更多的水推入水箱。这类似于导致电流增加的电压增加。
现在我们开始看到电压和电流之间的关系。但是,这里要考虑的第三个因素是:软管的宽度。以此类推,软管的宽度就是阻力。这意味着我们需要在模型中添加另一个术语:
- 水=电荷(以库仑为单位)
- 压力=电压(以伏特为单位)
- 流量=电流(以安培为单位,简称“安培”)
- 软管宽度=阻力
抵抗性
再次考虑我们的两个水箱,一个水箱较窄,另一个水箱较宽。

有理由认为,在相同的压力下,我们无法通过一个狭窄的管道容纳比一个更大的管道更大的容积。这就是抵抗。即使水与带有较宽管的水箱处于相同压力下,该较窄的管也会“阻止”通过它的水流。

在电气方面,这由具有相等电压和不同电阻的两个电路表示。电阻较高的电路将允许较少的电荷流过,这意味着电阻较高的电路将有较少的电流流过。
这使我们回到了乔治·欧姆。欧姆将“ 1欧姆”的电阻单位定义为导体中两点之间的电阻,施加1伏电压将推动1安培,即6.241×10 ^ 18个电子。该值通常在示意图中以希腊字母“Ω”表示,称为欧米茄,发音为“ ohm”。
欧姆定律
欧姆结合电压,电流和电阻的元素,得出了以下公式:

哪里
- V =电压(伏)
- I =电流(安培)
- R =欧姆电阻
这称为欧姆定律。例如,假设我们的电路的电势为1伏,电流为1安培,电阻为1欧姆。使用欧姆定律,我们可以说:

假设这代表我们的水箱上有一条宽软管。储罐中的水量定义为1伏,软管的“窄度”(流动阻力)定义为1欧姆。使用欧姆定律,这给我们提供了1安培的流量(电流)。
使用这个类比,现在让我们看一下带有窄软管的水箱。因为软管较窄,所以其流动阻力较高。让我们将此电阻定义为2欧姆。储水箱中的水量与其他储水箱中的水量相同,因此,使用欧姆定律,我们对软管较窄的储水箱的方程为

但是目前是什么?因为电阻更大,电压相同,所以我们得到的电流值为0.5安培:


因此,在具有较高电阻的储罐中电流较低。现在我们可以看到,如果我们知道欧姆定律的两个值,则可以求解第三个值。让我们通过实验来证明这一点。
欧姆定律实验
对于此实验,我们要使用9伏电池为LED供电。LED易碎,在烧坏之前只能流过一定数量的电流。在LED文档中,始终会有“电流额定值”。这是在特定的LED耗尽之前可以流过的最大电流。
所需材料
为了执行本教程结尾列出的实验,您将需要:
- 万用表
- 9伏电池
- 560欧姆电阻(或下一个最接近的值)
- LED灯
注意: LED是所谓的“非欧姆”设备。这意味着流过LED本身的电流的方程式不像V = IR那样简单。LED将一种称为“压降”的东西引入电路,从而改变流过电路的电流量。但是,在此实验中,我们只是试图保护LED免受过电流影响,因此我们将忽略LED的电流特性,并使用欧姆定律选择电阻值,以确保流经LED的电流安全地处于20mA
对于此示例,我们有一个9伏电池和一个红色LED,其额定电流为20毫安或0.020安。为了安全起见,我们宁愿不要以最大电流驱动LED,而要以其建议电流驱动它,该电流在其数据表中列为18mA或0.018安培。如果仅将LED直接连接到电池,则欧姆定律的值如下所示:

因此:

并且由于我们还没有抵抗力:

除以零会给我们无限的电流!好吧,实际上并不是无限的,而是电池可以提供的最大电流。由于我们不希望有太多电流流过我们的LED,因此需要一个电阻。我们的电路应如下所示:

我们可以以完全相同的方式使用欧姆定律来确定将为我们提供所需电流值的电阻值:

因此:

插入我们的价值观:

解决阻力:

因此,我们需要一个约500欧姆的电阻值,以将通过LED的电流保持在最大额定电流以下。

对于现成的电阻器,500欧姆不是一个常用值,因此,该设备将使用560欧姆的电阻器代替它。这是我们所有设备的外观。

成功!我们选择的电阻值要足够高,以使流经LED的电流保持在其最大额定值以下,但又要足够低,以使电流足以保持LED的美观和明亮。
该LED /限流电阻示例在业余电子产品中很常见。您通常需要使用欧姆定律来改变流经电路的电流量。在LilyPad LED板上可以看到这种实现方式的另一个示例。

通过这种设置,无需为LED选择电阻,该电阻已经随LED一起提供,因此可以实现电流限制,而无需手动添加电阻。
LED限流之前还是之后?
为了使事情更复杂一点,您可以在LED的两侧放置限流电阻,其工作原理相同!
许多人第一次学习电子产品时就遇到了这样的想法,即限流电阻可以在LED的任一侧使用,并且电路仍将照常工作。
想象一条连续不断的河,一条无限的,圆形的,流动的河。如果我们在其中放置水坝,整个河流将停止流动,而不仅仅是一侧。现在想象我们在河里放了一个水车,它减慢了河水的流量。将水车放置在圆圈中并不重要,它仍然会减慢整个河流的流量。
这是一个过分的简化,因为限流电阻无法放置在电路中的任何位置。可以将其放在LED的任一侧以执行其功能。
为了获得更科学的答案,我们转向基尔霍夫的电压定律。正是由于这一定律,限流电阻器可以在LED的任一侧穿过,但仍具有相同的效果。
资源和进一步发展
现在,您应该了解电压,电流,电阻的概念,以及这三者之间的关系。恭喜你!可以从欧姆定律直接导出用于分析电路的大多数方程和定律。通过了解这一简单定律,您将了解作为任何电路分析基础的概念!
,