一、探索性问题
是指对数学问题能在实验、猜想、合情推理的基础上,进行探索和研究,并予以证实;并能在新的情景中正确地表述数量关系,在创造性地思考问题的基础上,对较简单的问题得出一些新颖的结果。
例1 已知角α、β、
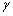
为锐角,且

,试求


的值。
解:这类求关系式的值的问题一般的解题策略为,先特值确定所求关系式的一个值,然后猜想所求关系的值为该值,再证明。
首先分别令α、β、都为

,

=1,于是猜想

的值为1。对猜想的结论进行证明:
证明:左边=

二、开放性问题
例2. 设函数

,若是偶函数,则t的一个可能值是__________。
解法1:由已知得

又因是偶函数
所以

所以

恒成立
所以

解法2:是由f(x)平移得到的,是偶函数,所以可以设

而

,所以t可以为

例3 已知函数

,试写出它的一个性质__________。
分析:中学数学讨论的函数性质有函数的定义域,值域(包括最大值和最小值),单调性,奇偶性,周期性等,函数是由两个十分常用的函数y=sinx和y=cosx组成,在同一坐标系中画出这两个函数的图像即可得到函数f(x)的图像,根据图像便可以讨论该函数的性质。
解:据该函数的图像(图像略)可以得到如下结论:
(1)此函数的定义域是R;
(2)该函数的值域是

;
(3)该函数是以2π为最小正周期的周期函数;
(4)当且仅当x=2kπ和x=

时,该函数取得最大值1;
(5)当且仅当

时,该函数取得最小值

;
(6)在

上是增函数,在

是减函数,在

上是增函数,在

是减函数。
以上各性质只需回答其一。
三、判断真假性问题
例4 采用如下方法判断函数

的奇偶性是否正确。


因为

是奇函数,所以f(x)是奇函数。
解:此解答是错误的。由于简化过程中约去了分子、分母的公因式

,使得

因定义域不同而不是同一个函数,故不能应用约分后的函数直接求约分前函数的奇偶性,本例的正确解答是:
令

,得一特解

的函数值。
因为

,而

无意义。
所以函数f(x)的定义域关于原点不对称。
故函数f(x)既不是奇函数也不是偶函数
四、模仿解答问题
例5 阅读下面例题解法:实数x、y满足

,

+

的值。
解:设

,化简后得:

解得

因为

所以

因为

所以

试用上述解法解下列问题:已知

求

的最大值。
解:因为


设

所以

因此当

时,M有最大值

五、运用方程思想解题的问题
例6 已知

。
分析:

,和同角三角比的关系式

联立形成一元二次方程求出

,这样

为一个一元二次方程的两个解,再求

。
解:因为
所以


因为

所以

是一元二次方程

的两个解。

,

,所以

。
例7 已知

且α为第三象限角,求sinα与cosα。
解:

,因为α为第三象限角
所以

由此可得

,

所以

的两个解
所以

六、追溯条件性问题
例8 请你写出一个关于α的等式并加以证明,要使得等式

是你给出的等式中当α=20°和α=15°时的情形。
分析:注意到这两个等式中三角比之间的运算方式相同,每个等式中的两个角之间都是相差30°,根据这些特征便可构建一个关于α和α+30°角所满足的等式。
解:命题:

证明:左边=


说明:归纳概括一系列数学等式所具有的共同性质,从而猜想并证明具有一般意义的数学结论,使得原有的结论成为特例,这种由特殊到一般的推广,是数学研究中常用的方法之一。
七、有关数学建模问题
例9 如图1,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花。若BC=α,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2。
(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求

取最小值时θ的值。

图1
解:(1)因为BC=a,∠ABC=θ
所以AB=acosθ,AC=asinθ,
所以

又因为

所以

所以

(2)


所以

有最小值,最小值为

八、在物理中的应用问题
例10 已知电流I与时间t的关系式为:

(1)图2是

在一个周期内的图像,P(

,0),Q(

,0),试根据图中数据求

的解析式;
(2)如果t在任意一段

秒的时间内,电流

都能取得最大值和最小值,那么ω的最小正整数值是多少。

图2
解:(1)

(2)因为

。
▍ 来源:综合网络
▍ 编辑:Wordwuli
▍ 声明:如有侵权,请联系删除;若需转载,请注明出处。