函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.而由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.函数的动点问题主要以几何图形为载体,运动变化为主线,集多个知识点为一体,集多种解题思想于一题. 这类题综合性强,能力要求高,它能全面的考查学生的实践操作能力,空间想象能力以及分析问题和解决问题的能力.
动态几何特点:问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。)动点问题一直是中考热点,研究它对于提升解决问题的能力有很大帮助.

类型1 与线段有关的问题
中考数学试题往往体现"六个维度",开放探究是其中之一,在探究性试题中,与线段有关的问题包括在点的运动过程中当某两条线段相等时,求运动时间;在点的运动过程中某条线段最大(或最小)时,求点的坐标;当某点是线段中点时,求动点的坐标等.
例1(2018·新疆乌鲁木齐)在平面直角坐标系xOy中,抛物线y=-1/4x² bx c经过
点A(-2,0),B(8,0).
(1)求抛物线的解析式;
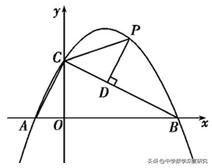
(2)点C是抛物线与y轴的交点,连接BC,设点P是抛物线上在第一象限内的点,PD⊥BC,垂足为点D.
①是否存在点P,使线段PD的长度最大?若存在,请求出点P的坐标;若不存在,请说明理由;
②当△PDC与△COA相似时,求点P的坐标.
【分析】(1)直接把点A(﹣2,0),B(8,0)代入抛物线的解析式中列二元一次方程组,解出b,c值可得结论;
(2)先得直线BC的解析式为:y=﹣1/2x 4,
①如图1,作辅助线,先说明Rt△PDE中,PD=PE•sin∠PED=PE•sin∠OCB=2√5/5 PE,则当线段PE最长时,PD的长最大,设P(t,1/4t² 3/2 t 4),则E(t,-1/2 t 4),表示PE的长,配方后可得PE的最大值,从而得PD的最大值;
②先根据勾股定理的逆定理可得∠ACB=90°,则△COA∽△BOC,
所以当△PDC与△COA相似时,就有△PDC与△BOC相似,分两种情况:
(I)若∠PCD=∠CBO时,即Rt△PDC∽Rt△COB,
(II)若∠PCD=∠BCO时,即Rt△PDC∽Rt△BOC,
分别求得P的坐标即可.
【解答】(1)把A(﹣2,0),B(8,0)代入抛物线y=﹣1/4x² bx c,
得:-1-2b c=0, -16 8b c=0,解得:b=3/2,c=4,
∴抛物线的解析式为:y=﹣1/4x² 3/2x 4;
(2)由(1)知C(0,4),∵B(8,0),
易得直线BC的解析式为:y=﹣1/2x 4,
①如图1,过P作PG⊥x轴于G,PG交BC于E,
Rt△BOC中,OC=4,OB=8,∴由勾股定理可求得BC=4√5,
在Rt△PDE中,PD=PE•sin∠PED=PE•sin∠OCB=2√5/5 PE,
∴当线段PE最长时,PD的长最大,
设P(t,-1/4t² 3/2t 4),则E(t,-1/2t 4),
∴PG=﹣1/4t² 3/2t 4,EG=﹣1/2 t 4,
∴PE=PG﹣EG=(-1/4t² 3/2t 4)﹣(﹣1/2 t 4)=﹣1/4t² 2t=﹣1/4(t﹣4)² 4,(0<t<8),
当t=4时,PE有最大值是4,此时P(4,6),
∴PD=2√5/5 ×4=8√5/5,
即当P(4,6)时,PD的长度最大,最大值是8√5/5;
②∵A(﹣2,0),B(8,0),C(0,4),
∴OA=2,OB=8,OC=4,
∴AC²=2² 4²=20,AB²=(2 8)²=100,BC²=4² 8²=80,
∴AC² BC²=AB²,∴∠ACB=90°,∴△COA∽△BOC,
当△PDC与△COA相似时,就有△PDC与△BOC相似,
∵相似三角形的对应角相等,
∴∠PCD=∠CBO或∠PCD=∠BCO,
(I)若∠PCD=∠CBO时,即Rt△PDC∽Rt△COB,
此时CP∥OB,∵C(0,4),∴yP=4,∴﹣1/4 t² 3/2t 4=4,
解得:x1=6,x2=0(舍),
即Rt△PDC∽Rt△COB时,P(6,4);
(II)若∠PCD=∠BCO时,即Rt△PDC∽Rt△BOC,
如图2,过P作x轴的垂线PG,交直线BC于F,
∴PF∥OC,∴∠PFC=∠BCO,∴∠PCD=∠PFC,∴PC=PF,
设P(n,﹣1/4n² 3/2 n 4),则PF=﹣1/4 n² 2n,
过P作PN⊥y轴于N,
Rt△PNC中,PC²=PN² CN²=PF²,
∴n² (﹣1/4n² 3/2 n 4﹣4)²=(﹣1/4 n² 2n )²,解得:n=3,
即Rt△PDC∽Rt△BOC时,P(3,25/4);
综上所述,当△PDC与△COA相似时,点P的坐标为(6,4)或(3,25/4).

方法规律:本题考查二次函数综合题、一次函数的应用、勾股定理的逆定理、锐角三角函数、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会根据方程解决问题,属于中考压轴题.
解答此类题目通常需要分析题目已知条件中的动点与定点以及动点与要研究的线段之间的关系.首先要明确哪些量是变化的,哪些量是不变的,用给定的自变量表示线段,再根据图形分析它们之间的关系.要"以静制动"即把动态问题转化为静态问题.在研究线段相等及线段长度之间的倍数关系,点为线段中点的问题时,要通过设未知数、建立方程、求解来解决问题.在研究点的运动过程中某条线段最大(或最小)的问题时,通常建立函数关系式,利用函数模型解决问题.在复习时要注意思维习惯,明确思路,逐步解决问题.此外,要注意解题方法的多样性.
高分秘籍:要使线段PD的长度最大,找到PD随PE的增大而增大的关系,写出PE与x的函数关系式是关键.

类型2 三角形存在性问题
近年来各省市大多以三角形存在性探究类试题作为压轴题,探究类试题突出特征是非常规,不是课本内容的简单模仿,需要更多的创造性,往往给出某种情境或某种实际需求,要求考生自己猜想结论,构建数学模型,解决问题,较全面考查学生的数学素养.探究三角形存在性问题,常见的有探究全等三角形的存在性、相似三角形的存在性、等腰三角形的存在性、直角三角形的存在性等.
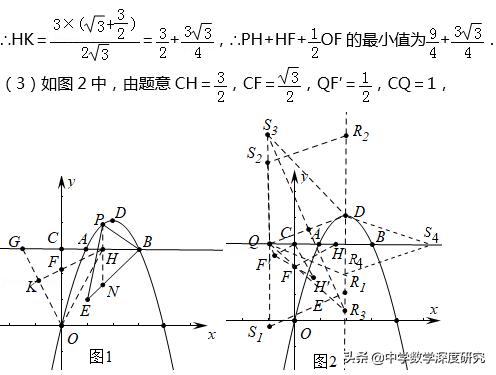
例2(2018·山东潍坊) .如图1,抛物线y1=ax ²﹣1/2x c与x轴交于点A和点B(1,0),与y轴交于点C(0,3/4),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
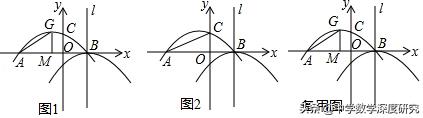
(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
分析: 由抛物线y1经过点B(1,0),C(0.3/4) ,利用待定系数法可以求得a,c的
值,得出y1的解析式.因为y2是由y1平移所得,且顶点为B(1,0),可以求得y2的解析式.△TAC为等腰三角形,需要进行分类讨论.点T为抛物线y2的对称轴上一点, 用勾股定理可以表示出TA ²,CA ²,CT ²,分三种情况分别建立方程,求解.同样,以P,Q,R为顶点的三角形与△AMG全等,也需要分类讨论,包括点P在直线l左侧和右侧两种情况,再分别讨论三角形的对应边,建立方程,求解.
【解答】(1)由已知,c=3/4,将B(1,0)代入,得:a﹣1/2 3/4=0,
解得a=﹣1/4,抛物线解析式为y1=﹣1/4x ²-1/2x 3/4,
∵抛物线y1平移后得到y2,且顶点为B(1,0),
∴y2=﹣1/4(x﹣1)²,即y2=﹣1/4x ²-1/2x-1/4.
(2)存在,如图1:
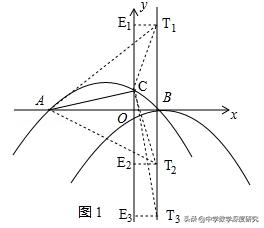
抛物线y2的对称轴l为x=1,设T(1,t),
已知A(﹣3,0),C(0,3/4),
过点T作TE⊥y轴于E,则
TC²=TE² CE²=1² (3/4-t) ²=t²-3/2 t 25/16,
TA²=TB² AB²=(1 3)² t²=t² 16,AC²=153/16,

(3)如图2:

设P(m,﹣1/4 m² -1/2 m 3/4),则Q(m,﹣1/4 m² 1/2 m-1/4)
∵Q、R关于x=1对称,∴R(2﹣m,﹣1/4 m² 1/2 m-1/4),
①当点P在直线l左侧时,PQ=1﹣m,QR=2﹣2m,
∵△PQR与△AMG全等,∴当PQ=GM且QR=AM时,m=0,
∴P(0,3/4),即点P、C重合.∴R(2,﹣1/4),
由此求直线PR解析式为y=﹣1/2 x 3/4,当PQ=AM且QR=GM时,无解;
②当点P在直线l右侧时,
同理:PQ=m﹣1,QR=2m﹣2,则P(2,﹣5/4),R(0,﹣1/4),
PQ解析式为:y=﹣1/2 x-1/4;
∴PR解析式为:y=﹣1/2 x 3/4或y=﹣1/2 x-1/4
方法规律: 本题是代数几何综合题,考查了二次函数性质、三角形全等和等腰三角形判定,应用了数形结合和分类讨论的数学思想.先假设存在,若题中已经给出用全等符号连接的两个三角形,则直接找对应边,转化为线段相等,进而求解;若题中没有给出用全等符号连接的两个三角形,则需要分类讨论对应边,进行求解.相似三角形存在性、等腰三角形的存在性、直角三角形的存在性的探究也需要类似的思考.
高分秘籍:假设存在,分类讨论,建立方程,准确求解是解决此类问题的关键.另外,画图观察有助于解决问题.

类型3 平行四边形存在性问题
近几年各省市中考试题注重探究性,压轴题以函数及几何图形的综合探究呈现,需要综合运用所学知识探究结论.这样的题目具有开放性、综合性,体现在假设存在以某些点为顶点的四边形是平行四边形,画出草图,观察判断.求涉及点的坐标时需要利用平行四边形的性质,建立方程,往往是方法开放,多数时候还需要分类讨论.
例3.(2018·重庆A卷)如图,在平面直角坐标系中,点A在抛物线y=-x² 4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).
(1)求线段AB的长;
(2)点P为线段AB上方抛物线上的任意一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当△PBE的面积最大时,求PH HF 1/2FO的最小值;
(3)在(2)中,当PH HF 1/2FO取得最小值时,将△CFH绕点C顺时针旋转60°后
得到△CF'H',过点F'作CF'的垂线与直线AB交于点Q,点R为抛物线对称轴上
的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S为顶点的四边形为菱形?若存在,请直接写出点S的坐标;若不存在,请说明理由.
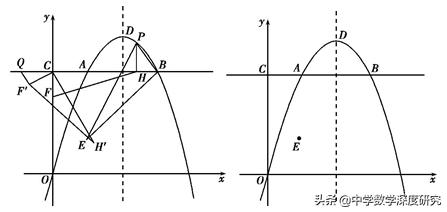
分析:将点A的横坐标代入抛物线的解析式可求得纵坐标,由点B与点A关于抛物线的对称轴对称可以得到线段AB的长;延长PH,交BE于点M,△PBE的面积可以看作△BPM与△EPM面积之和.因此,当PM取最大值时,S△PBE取最大值,可以确定点P与点H的坐标,进而求解;在(2)的基础上将△CFH绕点C顺时针旋转60°,按题目要求画出图形.分别以DQ为边、DQ为对角线画出菱形,由菱形的性质写出点S的坐标.
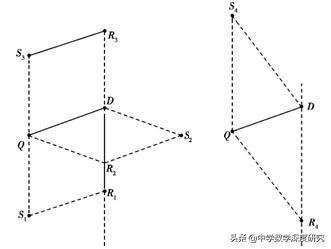
【解答】(1)由题意A(1,3),B(3,3),∴AB=2.
(2)如图1中,设P(m,﹣m ² 4m),作PN∥y轴J交BE于N.
∵直线BE的解析式为y=x,∴N(m,m),
∴S△PEB=1/2×2×(﹣m ² 3m)=﹣m ² 3m,
∴当m=3/2时,△PEB的面积最大,此时P(3/2,15/4),H(3/2,3),
∴PH=15/4﹣3=3/4,
作直线OG交AB于G,使得∠COG=30°,作HK⊥OG于K交OC于F,
∵FK=1/2OF,∴PH HF 1/2FO=PH FH FK=PH HK,
此时PH HF 1/2OF的值最小,
∵1/2•HG•OC=1/2•OG•HK,
∴Q(﹣1,3),D(2,4),DQ=√10,
①当DQ为菱形的边时,S1(﹣1,3﹣√10),S2(﹣1,3 √10),
②当DQ为对角线时,可得S3(﹣1,8),
③当DR为对角线时,可得S4(5,3)
综上所述,满足条件的点S坐标为(﹣1,3﹣√10)或(﹣1,3 √10)或(﹣1,8)或(5,3).
方法规律: 本题考查二次函数综合题、最短问题、菱形的判定和性质、解直角三角形、勾股定理等知识,解题的关键是学会构建二次函数解决最值问题,学会添加常用辅助线,根据垂线段最短解决最短问题,学会用分类讨论的思想思考问题,属于中考压轴题.
此类试题的解题方法首先要看题目,若要求的四边形是类似"以A,B,C,D为顶点的四边形"这样表述,就需要分类讨论,以AB为四边形的一边或以AB为对角线组成四边形.如果题目要求的四边形是类似"是否存在四边形ABCD是平行四边形"这样的表述,就不必分类讨论.利用平行四边形及特殊平行四边形的性质建立方程求解是解答此类题目的关键.复习时注意全面复习平行四边形的性质,有时利用平行四边形的对称性解题会更简单.
高分秘籍:探究平行四边形的存在性问题时,假设存在符合条件的平行四边形.通常有两类,一类是已知两定点求未知点的坐标,以两定点连线所成的线段作为探究平行四边形的边或对角线画符合题意的平行四边形;另一类是已知给定的三点求未知点的坐标,以这三点中的任意两个定点确定的线段为探究平行四边形的边或对角线画出符合题意的平行四边形.建立关系式,利用平行四边形的性质进行计算,也可以利用全等三角形、相似三角形的性质进行求解,还可以借助方程组解决问题.对于特殊平行四边形,要依据其性质解答问题.

类型4 最值问题
点的运动或图形的平移、旋转等变化,带来图形形状的变化,图形面积的变化,因此有了最值存在性问题.最值问题是探究两个变量之间关系的常见题型,如三角形面积最大值、四边形面积最大值、三角形周长最小值等.
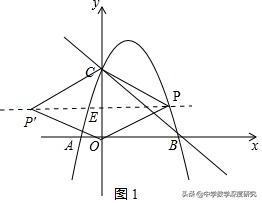
例4(2018·甘肃张掖)如图,已知二次函数y=ax ² 2x c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方抛物线上的一动点.
(1)求二次函数y=ax ² 2x c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP'C,若四边形POP'C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时点P的坐标和四边形ACPB面积的最大值.

分析:利用待定系数法求二次函数的表达式;由菱形的性质可知点P在OC的垂直平分线上,得出点P的纵坐标,利用抛物线解析式确定点P的横坐标;将四边形ABPC的面积看作△ABC、△PCQ、△PBQ的面积之和.设Q点坐标为(m,-m 3),写出四边形ABPC的面积与m的关系式,配方求得四边形ABPC的面积的最大值.
【解答】(1)将点B和点C的坐标代入函数解析式,得9a 6 c=0,c=3,
解得a=-1,c=3,所以二次函数的解析式为y=﹣x ² 2x 3;
(2)若四边形POP′C为菱形,则点P在线段CO的垂直平分线上,
如图1,连接PP′,则PE⊥CO,垂足为E,
∵C(0,3),∴E(0,3/2),
∴点P的纵坐标3/2,当y=3/2时,即﹣x ² 2x 3=3/2,
P在抛物线上,设P(m,﹣m ² 2m 3),
设直线BC的解析式为y=kx b,
将点B和点C的坐标代入函数解析式,得3k 3=0, b=3,
解得k=-1,b=3.直线BC的解析为y=﹣x 3,
设点Q的坐标为(m,﹣m 3),
PQ=﹣m ² 2m 3﹣(﹣m 3)=﹣m ² 3m.
当y=0时,﹣x ² 2x 3=0,解得x1=﹣1,x2=3,
OA=1,AB=3﹣(﹣1)=4,
S四边形ABPC=S△ABC S△PCQ S△PBQ
=1/2AB•OC 1/2PQ•OF 1/2PQ•FB
=1/2×4×3 1/2(﹣m ² 3m)×3
=﹣3/2(m﹣3/2)² 75/8,
当m=3/2时,四边形ABPC的面积最大.
当m=3/2时,﹣m ² 2m 3=15/4,即P点的坐标为(3/2,15/4).
当点P的坐标为(3/2,15/4)时,四边形ACPB的最大面积值为75/8.
方法规律:本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用菱形的性质得出P点的纵坐标,又利用了自变量与函数值的对应关系;解(3)的关键是利用面积的和差得出二次函数,又利用了二次函数的性质.
探究面积最值问题时常常需要建立该图形面积与某个自变量之间的函数表达式,求三角形的面积最值时,要用含自变量的代数式表示该三角形的底和高.求特殊四边形的面积最值时考虑直接代入公式,求任意四边形的面积最值时,则用割补法或将其分为两个三角形,用含自变量的代数式表示该四边形的面积.写出函数关系式后用配方法或二次函数的顶点公式求最值.还有利用两点之间线段最短或一次函数在取值范围内求最值的问题.
高分秘籍:将四边形的面积看作三个三角形面积之和,写出四边形面积与Q点横坐标的关系式是解决最值问题的关键.△PCQ、△PBQ都看作是以PQ为底边的三角形,两个三角形PQ边上的高的和为3.

牛刀小试:
1.(2018·湖北武汉) 抛物线L:y=﹣x2 bx c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式;
(2)如图1,过定点的直线y=kx﹣k 4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.

【答案】(1)y=﹣x ² 2x 1;
(2)k=﹣3;
(3)当m=2√2﹣1时,点P的坐标为(0,√2)和(0,2√2/3);
当m=2时,点P的坐标为(0,1)和(0,2).
【提示】(1)根据对称轴为直线x=1且抛物线过点A(0,1)求解可得;
(2)根据直线y=kx﹣k 4=k(x﹣1) 4知直线所过定点G坐标为(1,4),

(3)设抛物线L1的解析式为y=﹣x² 2x 1 m,知C(0,1 m)、D(2,1 m)、F(1,0),再设P(0,t),分△PCD∽△POF和△PCD∽△POF两种情况,由对应边成比例得出关于t与m的方程,利用符合条件的点P恰有2个,结合方程的解的情况求解可得.

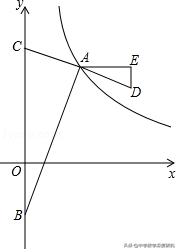
2. 如图,在平面直角坐标系xOy中,点A是反比例函数y=(m ³-m ²)/x (x>0,m>1)图象上一点,点A的横坐标为m,点B(0,﹣m)是y轴负半轴上的一点,连接AB,AC⊥AB,交y轴于点C,延长CA到点D,使得AD=AC,过点A作AE平行于x轴,过点D作y轴平行线交AE于点E.
(1)当m=3时,求点A的坐标;
(2)DE=_____ ,设点D的坐标为(x,y),求y关于x的函数关系式和自变量的取值范围;
(3)连接BD,过点A作BD的平行线,与(2)中的函数图象交于点F,当m为何值时,以A、B、D、F为顶点的四边形是平行四边形?
【答案】(1)点A坐标为(3,6)
(2)DE=1,y=1/4 x ²-1/2 x-1(x>2)
(3)当m=2时,以A、B、D、F为顶点的四边形是平行四边形.
【提示】(1)根据题意代入m值;
(2)利用ED∥y轴,AD=AC构造全等三角形将求DE转化为求FC,再利用三角形相似求出FC;用m表示D点坐标,利用代入消元法得到y与x函数关系.
(3)数值上线段中点坐标等于端点坐标的平均数,坐标系中同样可得线段中点横纵坐标分别是端点横纵坐标的平均数,利用此方法表示出F点坐标代入(2)中函数关系式即可.

以上几个问题都是以平面直角坐标系为平台,以直线、抛物线为主线,以动点或动图为探究点而构成的代数、几何综合探究问题,突出了函数、方程、数形结合和分类讨论等基本数学思想方法,解题时关注了运动和变化过程中不变量、不变关系和特殊关系,以此打破突破口,使问题得以解决。
解决此类与运动、变化有关的问题,重在运动中分析,变化中求解.首先,要把握运动规律,寻求运动中的特殊位置,在"动"中求"静",在"静"中探求"动"的一般规律.其次,通过探索、归纳、猜想,获得图形在运动过程中是否保留或具有某种性质,要用运动的眼光观察出各种可能的情况分类讨论,较为精确地将每种情况一一呈现出来.再次,要学会将动态问题静态化,即将动态情境化为几个静态的情境,从中寻找两个变量间的关系,用相关字母去表示几何图形中的长度、点的坐标等,很多情况下是与三角形的相似和勾股定理等联系在一起的,在整个解题过程中,要深刻理解分类讨论、数形结合、化归、相似等数学思想.
,