
一、对称性的分类

对称,简单来说就是图形在某种变换条件下(例如旋转、折叠等),其相同部分间有规律的重复。如图1、图2
在考试中往往会将图形进一步分类,主要分为两种类型:(1)轴对称图形;(2)中心对称图形。轴对称指图形只要沿着图形中一条线对折能够完全重合,就叫轴对称图形。
例如图1就是典型的轴对称图形,除此之外,还有五角星、等边三角形等等。中心对称是指把一个图形绕着中心一点旋转180°,如果它能与原图形重合,那么就说这个图形是中心对称图形。例如图2、S、%、等图形。
对于图形中心对称与轴对称的考察往往是在分组分类题中出现,让考生根据对称性的不同将其分成两组,一组是轴对称图形,一组是中心对称图形。如2014年国考题中给出的这副图形(图3)
这道题就属于分组分类题,给出六幅图形让考生根据他们的特点分为两组,每一组图形的特征要一致。通过观察可以发现六幅图形相同点均为对称图形,但由于其对称性有所不同,进一步可以将其分为两组,一组是①④⑥为轴对称图形,一组是②③④为中心对称图形。
在对称图形中对中心对称与轴对称的考察是其最为常见的考法,但其并不局限于图形中,在关于汉字和字母的图形推理中也可能出题,例如:汉字“”为中心对称,字母“”为轴对称。

二、轴对称图形之对称轴方向
在做题中,有同学问:“如果题干中给出的对称图形都是轴对称图形那怎么办呢?”。那这时考的往往不是对称性的分类了,而有可能考察的是轴对称图形之对称轴方向。对称轴方向的考察主要有两种方式:(1)横轴对称、竖轴对称与斜轴对称;(2)对称轴角度变化。轴对称图形中折痕所在的直线叫做它的对称轴。根据直线的方向不同,轴对称图形进一步分为横轴对称、竖轴对称与斜轴对称。如2016国考题(图4)
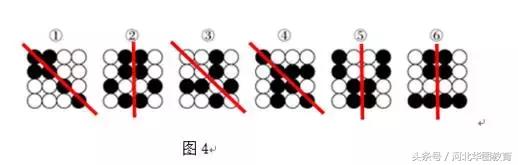
刚看到题,很多同学都会想到数黑球或白球的数量,但是并没发现明显规律。图形局部数量没有规律,故而要从图形整体观察。此题中,所有图形均为轴对称图形,对称轴如图4所示,6幅图形均有一条对称轴,只是对称轴方向不同,故可以根据对称轴的方向不同分为两组。其中①③④为一组,图形都是斜轴对称,②⑤⑥为一组,图形为竖轴对称。
如果一组图形除了都是轴对称图形之外,其对称轴方向还变化多样(不只是横轴与竖轴或竖轴与横轴,有3种或3种以上方向),那么还有可能考察对称轴角度的变化规律。如2017国考题(图5)

图5中图形均为含有1条对称轴图形,图形之间只是对称轴方向不同。可以观察到他们对称轴从左到右依次顺时针旋转45°。按照此规律,后面应该选择一个对称轴方向为“ ”的图形。
所以,如果一组图形都是轴对称图形,且均只有一条对称轴,这时首先应观察图形看其对称轴方向是不是一致,如果一致可以根据对称轴方向分组分类;如果对称轴方向不一致,则需要将所有图形对称轴连在一起观察,往往会发现其对称轴在做旋转运动,根据转动的角度不同总结规律推理出答案。

三、轴对称图形之对称轴数量
轴对称图形中,对称轴数量为1条时往往考察对称轴方向变化。但如果图形中对称轴数量不同,又考的什么呢?那这时非常有可能考察对称轴数量变化,最常见的就是根据对称轴的数量,即1条、2条、3条分组分类。如2015国考题(图6)

图6中所有图形也均为轴对称图形,但是仔细观察会发现他们的对称轴数量并不一致。从①到⑥图形,对称轴数量依次为3、3、1、1、3、1,图形①②⑤均有3条对称轴;③④⑥均有1条对称轴。因此可以根据对称轴的数量不同分为两组。
在考察对称轴数量的考题中,一般来说,会给出对称轴非常明显且数量不会太多的图形。纵观历年真题,关于图形对称轴数量的考察,最多为3条,而且出题形式主要以分组分类题为主。因此,如果一个图形的对称轴数量如果超过4条及以上一般不会优先考虑对称轴的数量;如果图形中对称轴数量不同,且≤3条,优先考虑根据对称轴数量不同分组。
通过上述的分析,可以总结出在解图形推理题时应该遵从下面几步走:首先,观察图形之间相同点确定考察方向。如果图形都是对称图形,那么就很可能考察其对称性。其次,根据图形之间不同点确定考点。如果图形有轴对称、中心对称,那可能是要求根据对称性不同分组分类。如果图形都是轴对称,则要根据对称轴数量是否相同判定考点;如果对称轴数量相同,则考对称轴方向变化;如果对称轴数量不同,很可能让考生根据不同数量对称轴分组分类。
文章来源华图教育,转载请注明

今天的“货”很“干”。嗯,不知道大家适不适应。技巧当然是越详细越好,但是说到做题,还是需要大家平时多做题了。多做题国考肯定就不咸鱼!
,




