接上篇:你也能懂的微积分(上)
微积分的发明使我们求曲线围成面积的难度出现了断崖式的下降。那么,在这个过程中到底发生了什么?为什么数学可以如此有效地简化我们的问题?是我们的问题本来就很简单,以前把它想复杂了,还是我们真的把问题的复杂度降低了?
还记得小学遇到的“鸡兔同笼”问题么?鸡和兔被关在一个笼子里,从上面数,一共有35个头,从下面数,一共有94只脚,请问笼子里分别有多少只鸡和兔?

有很多“聪明”的老师会教你一些非常“有用”的解题技巧,比如,因为鸡有一个头两只脚,兔子有一个头四只脚,而现在总共有35个头,那么你把这个35乘以2,得到的70就是所有的鸡的脚加上一半的兔子的脚(因为兔子有4只脚,而你只乘以2,所以每只兔子你还有2只脚没有算)。
然后,我用总脚数94减去这个70,得到的24就是剩下的一半兔子脚,再用24除以2(一只兔子4只脚,一半就是2只)就得到了兔子的数量12。因为一共有35个头,那么用35-12=23就是鸡的数量。
当然,鸡兔同笼问题还有很多其它的特殊解法,长尾君这里就不再列举了。这些解法算出来的结果有问题吗?当然没问题,但是这些解法简单么?好么?
不好!为什么?因为局限性太大了。我今天放鸡和兔你可以这样算,那明天我要是放点其它的动物这方法是不是就不管用了?如果下次不是数头和脚,而是去数翅膀和脚,这方法还行么?
这就跟阿基米德用穷竭法算曲线围成的面积一样,面对每一种不同曲线围成的面积,我求面积的方法都不一样。我的每一种解法都严重依赖曲线的具体特性,所以这种方法的局限性就非常大,带来的意义也非常有限。
而微积分之所以伟大,就是因为它从这些看起来不一样的问题里抽象出来了一个共同的本质,然后所有的问题都可以套用这套程序,这样大家才能放心的以它为跳板往前冲。
后来我们学习了方程,接着就发现以前让我们头痛不已的“鸡兔同笼”问题突然就变得非常简单了。不仅解决这个具体问题简单,而且随便你怎么变化,加入其它的动物也好,数上翅膀也好,都可以用一样的程序闭着眼睛把题目做出来。为什么会这样?
没有方程的时候,我们得具体问题具体分析,然后根据它的题干去做各种逆向分析。
逆向思考,这本来就是很反人类的思维方式。我们很容易从一系列原因出发得到某种结果,但是给你某种结果让你去倒着分析原因就是很困难的事情了(这不才有了侦探这个职业么)。

比如,如果我们现在知道了有23只鸡,12只兔子,然后让你去计算有多少头和脚,这是正向思维,很容易。但是,如果告诉你有多少头和脚,让你去反着思考有多少鸡和兔子,这就是逆向思维了,很麻烦。
方程告诉我们:为什么放着自己熟悉的正向思维不用,而跑去用麻烦的逆向思维呢?你说,我这不是不知道有多少只鸡和兔子,这不得已才用逆向思维么?方程告诉你,你不知道有多少只鸡和兔子无所谓,你可以先用一个未知的量代替它,先用正向思维把方程列出来再说。
比如,我假设有x只鸡,y只兔子,那么,一共就有x y个头,2x 4y只腿。而题目告诉我们有35个头,94只脚,所以我们就可以得到:
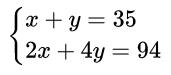
我们毫不费力的就把这两个方程列出来了,于是这个题目基本上就做完了。因为剩下的事情就是把x和y从方程里解出来,而解方程是一件高度程序化的事情,什么样的方程怎么去求解,都有固定的方法。
从小学时代的“聪明技巧”到傻瓜式地列方程、解方程,这是数学上一个非常典型的进步,大家可以仔细想想:这个过程中到底发生了什么?方程到底是如何简化问题的?这跟微积分的发明有何异曲同工之妙?
其实,我们开始思考鸡兔同笼的那些“聪明的技巧”,那些逆向思维时的思路,都被打包塞到解方程的步骤里去了。
什么意思?比如,你要解上面这个方程:
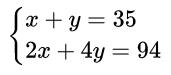
老师可能会教你一些固定的方法。
第一步,把方程1两边都乘以2,得到2x 2y=70(这不就是跟我们上面的方法一样,把所有鸡兔的头都乘以2么)。
第二步,再用方程2减去方程1,这样就把x消去了,得到了2y=24(我们上面也是这么说的,脚的数量减去2倍头的数量就等于兔子剩下的脚的一半),然后就把兔子的数量y=12求出来了。
第三步,把兔子的数量,也就是y的值12代入到方程1,求出x的值,得到了鸡的数量23。
大家发现没有:你以前思考这个问题时最复杂的那些步骤,现在完全被机械化地打包到解方程的过程中去了。你以前觉得那些只有你才能想得到的巧妙解题技巧,只不过是最简单的解方程的方法,所以你就觉得这个问题现在变得非常简单了。
这就是数学!

数学不断地从不同领域抽象出一些相同的本质,然后尽可能地把抽象出来的东西一般化,程序化,这样我们就能越来越方便地掌握各种高级数学武器。
因此,数学越发展越抽象,越看重这种能够一般化、程序化的解决某种问题的方法。所以,方程的思想是革命性的,微积分也一样。
微积分也是使用了一种通用的方法来处理各种曲线围成的面积,稍加变化我们就能同样求出曲线的长度,或者曲面包含的体积。微积分之所以能够简化求面积的逻辑,是因为微积分把这块逻辑都打包到求原函数里去了,而后者是一个可以程序化、一般化的操作。
所以,我们学习数学的时候,也要更多地注意这些数学是从哪些不同的地方抽象出了哪些相同的本质,如何一般化地解决这类问题上。这是数学的“大道”,我们不用过于在意那些小技巧,没必要耗时间去琢磨“鸡兔同笼”问题的108种解法,以至于拣了芝麻丢了西瓜~
这一段似乎有点偏离主题,但是我觉得很重要。把这些理清楚了,对大家如何定位数学,如何理解、学习数学都会有很大的帮助。否则,如果我们从小学到高中学了十几年的数学,却不知道数学是什么,那不是很悲催么?而且,这一段对于我们理解微积分的意义也会很有帮助。
好,现在微积分创立了,微积分的基本定理也被正式地提出来了,接下来应该再做什么呢?你该不会以为文章到这里就要结束了吧?不不不,还远远没有。
诚然,微积分基本定理的发现是这场革命里最核心的东西,相当于革命的指导思想。既然已经有了指导思想,那接下来要做的事情自然就是扩大战果,把这么优秀的思想扩散到各个领域里去啊。怎么扩呢?
首先,微积分基本定理的核心思想就是用求原函数的方式来解决求面积的问题,所以求一个函数的原函数就成了问题的核心。那么,我们自然就要研究各种常见函数的求导和求原函数的方法。
这些弄清楚之后,我们接下来就要问:由一些常见函数组成的复合函数,比如两个函数相加减、相乘除、相嵌套复合等时候要怎么求原函数?怎么求积分?再扩展一下,现在知道了如何求面积,那要怎样求体积,求曲线的长度呢?
这部分内容是我们最擅长的,也是我们考试的重点。它的核心就是熟悉各种前人总结下来的微积分技巧,多练习,熟能生巧,没什么捷径。但是,也要特别警惕把对微积分的学习完全变成了对这种技巧的训练,这样数学就真的变成了算术了。
此外,我强烈建议有抱负的同学不要急着打开微积分的课本直接去翻看这些问题的答案。我在前面已经把微积分的思想说了,大家完全可以看看自己能不能独立把这些问题推出来,实在没辙了再去翻课本,也就是孔子说的“不愤不启,不悱不发”。

像牛顿和莱布尼茨那样洞察“积分和微分是互逆运算”,然后提出微积分基本定理,这是一流科学家的素养。一流科学家提出这种重大创新之后,你能跟着把后面很自然的东西做完善,这是二流科学家的基本素养。大家在学习数学的时候要有意识地培养自己的这种能力~
然后,我们就可以把微积分的技术扩展到各种其它的领域了。比如,有了微积分,我就可以研究弯曲的东西,曲线、曲面什么的都可以研究。这就等于说是在用微积分来研究几何,这就是微分几何。后面我讲广义相对论的时候,这玩意就必不可少了。
有了微积分,我们发现很多物理定律都可以写成微分方程的形式,有多个变量的时候就是偏微分方程。我上三篇文章讲的麦克斯韦方程组、波动方程,后面要讲的广义相对论的场方程,都是这样。
有了微积分,我们就可以计算各种不同曲线的长度。那么,如何确定在特定条件下最短的那条曲线呢?这里就发展出了变分法,变分法配合最小作用量原理,在物理学的发展里起到了极为关键的作用。

所以,微积分在接下来的两个世纪里基本上就这样疯狂的扩张着。科学(尤其是物理学)的发展需要微积分,微积分也需要从科学里寻汲取营养,它们就这样相互促进、相互成长、相亲相爱。
但是,似乎大家都忘了一个问题:此时微积分的基础并不牢固,莱布尼茨把dx视为一个无穷小量,但是无穷小量还是怎么说都说不圆。
一个接近于0又不等于0的无穷小量到底是个什么玩意?为什么你有时候可以把它当除数约掉(认为它不为0),有时候又随意把它舍弃(认为它等于0)?看数学史的时候也会觉得奇怪,像欧拉、拉格朗日、拉普拉斯、伯努利兄弟这些顶级数学家,居然都对这些问题视而不见。更让人奇怪的是,他们使用这种逻辑不严密的微积分居然没有出什么差错,只能说大佬们的直觉确实逆天。

因此,微积分最后的问题就是:如何使微积分严密化?如何把微积分建立在一个坚实的基础之上?
之所以把dx看成一个无限趋近于0却又不等于0的无穷小量,主要是因为这样做很直观。我们用很多矩形去逼近曲线围成的面积,矩形数量越多,每个矩形的宽度就越小。当矩形的数量变成“无穷多个”的时候,每个矩形的宽度就“理所当然”地变成了无穷小。这么看,无穷小量确实很直观,但是这里有什么问题呢?
当我说矩形的数量是一百个、一千个的时候,我是可以把它们都数出来的,我也可以把它们的面积之和都算出来。但是,当你说矩形的数量是无穷多个的时候,无穷多个是多少个?你能数出来么?你真的可以把无穷多个矩形的面积一一算出来,然后把它们加起来么?
有人可能觉得我在胡搅蛮缠。无穷嘛,那肯定是无法具体数出来、测出来的,也不可能真的把无穷多个矩形的面积一个个算出来再求和。但是我知道是那么个意思,是那么回事就行了。我测不出来,但是我能想出来,难道还不让我想了么?
对,还真就不让想了!
大家可能都知道,科学和哲学以前是一家的。因为纯粹的思辨在哲学里非常常见,所以以前的“科学”里就到处夹杂着这种“可以想但是无法测量的东西”,这就极大的限制了科学的发展。因为一个东西如果无法测量你就无法用实验去验证它,无法验证你就不知道它是对是错,你不知道对错那就只能以权威说了算。你没有证据还敢说权威不对,那就很麻烦了,所以亚里士多德的学说可以统治欧洲近两千年。
现代科学从哲学里分离了出来,一个标志性的操作就是:科学家们开始关注那些能够用实验测量到的量,对那些用实验无法测量的东西避而不谈。
伽利略是公认的“现代科学之父”,他的核心观点有两条:第一,用数学定量地描述科学;第二,用实验验证科学。所以,如果你谈的是现代科学,那你就不能乱想了。
如果你还想用一些无法测量的概念来构建你的“科学体系”,那么你的方法论就是非科学的,你构建的也只是玄学而非科学,这是很多民科非常容易犯的错误。庞加莱甚至直接说:“凡是不能测量的东西,都不能算是自然科学。”

这种思想在科学昌盛的19世纪已经很普遍了,诞生于这个时期的实证主义也指出:人类不可能也不必要去认识事物的“本质”,科学是对经验的描写。他们甚至提出口号要“取消形而上学”。
总之,一切的一切就是不让你在科学里再谈那些无法测量,无法验证的概念,科学要基于实证。
那么,只能想却无法数,无法“观测”的无穷小量是不是这样的一个概念呢?虽然它很直观,但是你回顾科学的历史,反直觉的重大科学进步难道还少么?历史一次次地告诫我们:直觉不可靠,我们能依靠的只有严密的逻辑和确凿的实验。
在这样的大环境下,我们迎来了一位重要人物:柯西。

柯西深刻地认识到:只要涉及数学概念,任何关于连续运动的一些先验的直观观念,都是可以避免,甚至是必须避免的。科学放弃了形而上学方面的努力,采用“可观测”概念之后就迎来了大发展,那数学为什么不也这样呢?
无穷小量是一个无限趋近于0但是又不能等于0的概念,也就是说它有一个极限位置0,你可以想多接近就多接近,但就是无法到达。
我们知道实数跟数轴上的点是一一对应的。当我们说一个量在无限趋近于0的时候,很多人脑海里浮现的画面就是一个点在数轴上不停地移动,从一个点移动到下一个点,一直靠近0这个点。
但是这个图景是不对的,为什么?因为实数是稠密的。稠密就是说任意两个点(实数)之间永远都有无数个点(实数)(你自己想想是不是,1和2之间有多少个数?)。你以为它能从A点移动到邻近的下一个B点么?对不起,这个它真做不到!
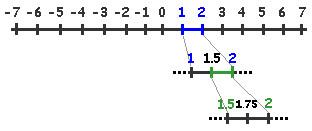
A点和B点之间永远有无数个点,也就是说A点根本就没有所谓的“下一个点”。你认为我一定要走完了A点到B点之间所有的点才能到达B点,那就不可避免地会陷入到芝诺悖论里去。因为你压根就不可能走完任何两个点之间的所有点(因为是无穷多个),所以,如果按照这种逻辑,你就根本“走不动”,所以芝诺的飞矢就飞不动了。

因此,面对这种连续的概念的时候,我们就不应该使用这种“动态的”定义。你想通过“让一个点在数轴上动态地运动来定义极限”是行不通的,这就是莱布尼茨的无穷小量栽跟头的真正原因。
数学家们经过一百多年的探索、失败和总结,最后终于意识到了这点,这些思想在柯西这里完全成熟。于是,柯西完全放弃了那种动态的定义方式,转而采取了一种完全静态,完全可以描述测量的方式重新定义了极限,进而为微积分奠定了扎实的基础。
这里我把柯西对极限的新定义原封不动的贴出来:当一个变量相继的值无限地趋近某个固定值的时候,如果它同这个固定值之间的差可以随意地小,那么这个固定值就被称为它的极限。
有人看了这个定义之后就在犯嘀咕:这跟莱布尼茨说的不是一样的么?你还不是在用“无限趋近”啊,“随意的小”啊这种跟“无穷小”差不多的概念来定义极限么?你说以前的定义是动态的,柯西给整成了静态的,可是我看来看去,柯西这个定义好像也在动啊。什么无限趋近,随意的小,不是在动么?
有这些疑问是正常的,毕竟是让数学家们卡了一百多年的问题,不可能那么太“显而易见”。
我们再仔细看看柯西的定义,它跟以前的差别到底在哪?你看啊,柯西虽然也有用“无限趋近”,但是他只是用这个来描述这个现象,并不是用它来做判决的。他的核心判决是后面一句:如果它同这个固定值之间的差可以随意的小,那么它就是极限。
可以随意的小和你主动去无限逼近是完全不一样的。可以随意小的意思是:你让我多小我就可以多小。你让我小于0.1,我就能小于0.1;你让我小于0.01,我就能小于0.01;你让我小于0.00…001,我就可以小于0.00…001。只要你能说出一个确定的值,不管你说的值有多小,我都可以让它跟这个固定值的差比你更小。柯西说如果这样的话,那么这个固定值就是它的极限。
大家发现没有,柯西学聪明,学鸡贼了,他把这个判断过程给颠倒了过来。以前是你要证明自己的极限是0,你就不停地变小,不停地朝0这个地方跑过去。但是,你和0之间永远隔着无数个点,所以你永远也跑不完,你也就不知道你要跑到什么时候去,这样就晕了。
现在我学聪明了,这个难以界定的东西,这个烫手的山芋我不管了,我丢给你,我让你先说。只要你说出一个数,你要我变得多小我就变得多小。你如果想让我变成无穷小,那你就得先把无穷小是多少给我说出来,你说不出来的话那就不能怪我了。

完美甩锅!这就是柯西的核心思想。
柯西就通过这种方式把那些不可测的概念挡在了数学之外,因为你能具体说出来的数,那肯定就都是“可观测”的啊。大家再看看这个定义,再想想之前莱布尼茨的想法,是不是这么回事?
于是,柯西就这样完美的甩开了那个招人烦的无穷小量。在柯西这里,无穷小量不过就是一个简单的极限为0的量而已,一个“只要你可以说出一个数,我肯定就可以让我和0之间的差比你给的数更小”的量。这样我们就能把它说得清清楚楚,它也不再有任何神秘了。
然后,魏尔斯特拉斯用完全数学的语言改进了柯西的这段纯文字的定义,得到了最终的,也是我们现在教材里使用的ε-δ极限定义。
根据柯西的思想,魏尔斯特拉斯说:你要判断某个函数f(x)在某个地方a的极限是不是某个值L,关键就要看如果我任意说一个数ε(比如0.00…001或者任意其它的,注意是任意取,这里用ε代替),你能不能找到一个x的取值范围(用δ来衡量),让这个范围里的函数值f(x)与那个值L之间的差(用套个绝对值的|f(x)-L|表示)小于ε。如果你总能找到这样的δ,那我就说函数f(x)在a点的极限为L。
用精练的数学语言表述上面的话就是:当且仅当对于任意的ε,存在一个δ>0,使得只要0<|x-a|<δ,就有|f(x)-L|<ε,那么我们就说f(x)在a点的极限为L。记做:

定义里的Lim就是极限的英文单词Limit的缩写,这个箭头x->a也非常形象地表达了极限这个概念。
这个定义就真正做到了完全“静态”,不再有任何运动的痕迹(连柯西说的“无限趋近”、“随意的小”都没有了),也不再有任何说不清的地方。从定义你也能清楚地看出来:它根本不关心你是如何逼近L的,飞过去、跳过去、爬过去的它都不管,只要最后的差比ε小就行,我就承认你是我的极限。
用一位伟人的名言翻译一下就是:不管黑猫白猫,能比ε还小的就是我的极限好猫。

这里要特别注意的是ε是任意的,任意就是说随便ε取什么你都要找到对应的δ,你不能说有10个ε满足条件就说这是极限。
看个例子,我们考虑最简单的f(x)=1/x。当x的取值(x>0)越来越大的时候,这个函数的值就会越来越小:
f(1)=1,
f(10)=0.1,
f(100)=0.01,
f(1000)=0.001,
……
看得出来,当x的取值越来越大的时候,f(x)的值会越来越趋近于0。所以,函数f(x)在无穷远处的极限值应该是0,也就是说:

这个结论是很明显的,接下来我们就来看看如何用ε-δ定义来说这个事。
按照定义,我们要取一个任意小的ε,假设这里我们取ε=0.1,那么我们就要去找一个δ,看能不能找到一个范围让|f(x)-0|<0.1,显然只需要x>10就行了;取ε=0.01,就只需要x>100就行了;任意给一个ε,我们显然都能找到一个数,当x大于这个数的时候满足|f(x)-0|<ε,这样就OK了。
于是,我们就构建了一个逻辑严密,不再有任何“说不清”概念的极限理论。有了这个坚实的地基,我们就可以放心地在上面盖房子了。那个漂泊了一百多年,那个被幽灵般的无穷小量缠绕了一百多年的微积分,即将迎来新生。
先看积分,我们之前认为曲线围成的面积是无数个宽度为无穷小量的矩形面积之和,于是我们在这里就被无穷小量缠上了。有了ε-δ极限之后,我们就可以刷新一下我们对积分的认知了:从现在起,我们把曲线围成的面积看成是一个极限,而不再是无数个无穷小量的矩形面积之和。
什么意思?假设我们用1个矩形逼近曲线围成的面积的时候,我把这一个矩形的面积记做S1,用两个矩形逼近的面积之和记做S2,同样的,我们记下S3,S4,S5……
一般情况,如果我们用n个矩形去逼近这个面积,这n个矩形的面积之和就记做Sn。如果这个Sn的极限存在,也就是说,随便你说出一个数字ε,我都能找到一个n的范围,让Sn和A之间的差|Sn-A|小于你给定的这个数字ε。那么,A就是这个Sn的极限。

于是,我们就说:曲线围成的面积就是这个极限A,它是n个矩形面积之和这个序列Sn的极限。

所以,我们就把这个极限过程表示的面积A定义为函数f(x)从a到b上的积分:

这样,我们的积分就成了一个由ε-δ语言精确定义的极限。这里没有那个等于0又不等于0的无穷小量,一切都清清楚楚、明明白白,没有含糊的地方,这就是第二次数学危机的终极解决之道。
这样处理虽然不再那么直观,但是它非常精确和严密,这是符合数学的精神的。直观虽然能帮助我们更好的感受数学,但是如果失去了严密性,数学将什么都不是。
积分解决了,微分这边也是一样。有了ε-δ定义之后,我们就再不能把导数看成是两个无穷小量的比值(dy/dx),而是:把导数也看成一个极限,对,还是极限。
这个理解起来相对容易,函数在某一点的导数就是这点切线的斜率。我们前面也说了,切线就是当割线的两点不停地靠近,当它们的距离变成无穷小时决定的直线。
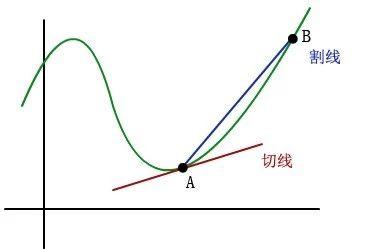
很显然,这个定义是依赖无穷小量的,我们现在要用ε-δ定义的极限来代替这个无穷小量。所以,切线就应该被理解为割线的极限,那么切线的斜率(也就是这点的导数)自然就是割线斜率的极限,所以导数f(x)’也自然而然地成了一个极限。
由于割线的斜率就是用这两点的纵坐标之差f(x Δx)-f(x)除以这两点的横坐标之差(x Δx-x=Δx),而导数f(x)’是割线斜率的极限。那么,我们在割线斜率的前面加一个极限符号就可以表示导数f(x)’了:

这才是导数的真正定义,它是一个极限,而不再是两个无穷小量dy与dx的商dy/dx。也就是说,按照极限的ε-δ定义,这个导数f(x)’的真正含义是:你任意给一个ε,我都能让割线的斜率与这个值的差比你给的ε更小。
我反复强调ε-δ定义的含义,就是希望大家能真的从这种角度去理解极限,思考极限,逐渐放弃那种“无限动态趋近某个点”的图景。思维一旦形成定势,想再改过来是非常困难的,所以我们得经常给自己“洗脑”,直到把新理论的核心思想洗到自己的潜意识里去,这样才算真正掌握了它。
我以前讲相对论的时候,很多人在讲相对论时能切换到相对论思维,但是平常一不留神就又跌回到牛顿的思维里去了。然后就闹出了一堆悖论、佯谬和各种奇奇怪怪的东西,这里也一样。
莱布尼茨当年认为导数是两个无穷小量dy和dx的商,所以他用dy/dx来表示导数。虽然现在导数不再是这个意思,但是莱布尼茨当年精心发明的这一套符号确实是非常好用,于是我们就继续沿用了下来。
也就是说,我们今天仍然用dy/dx表示导数,但是大家一定要注意,dy/dx在现代语境里是一个极限,不再是两个无穷小量的商。
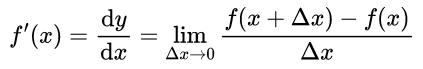
如果不熟悉微积分的历史,就很容易对这些符号产生各种误解,这也是很多科普文、教科书在讲微积分时的一大难点。因为思想是新的,符号却是老的,确实很容易让人犯糊涂。
于是,在莱布尼茨那里,他是先定义了代表无穷小量的微分dx和dy,然后再用微分的商定义了导数dy/dx,所以那时候导数也叫微商。

但是现在剧情完全反转了:我们现在是先用ε-δ定义了极限,然后从极限定义导数dy/dx。这里压根没有微分什么事,只不过由于历史原因我们依然把导数写成dy/dx这个样子。
那么,dx和dy这两个之前被当作无穷小量的微分的东西,现在还有意义么?
答案是有意义!
这个dx和dy还是有意义的,当然,有意义也肯定不可能再是以前无穷小量的意思了。那么,在ε-δ极限这种全新的语境下,dx和dy在新时代的意义又是什么呢?请看下图:
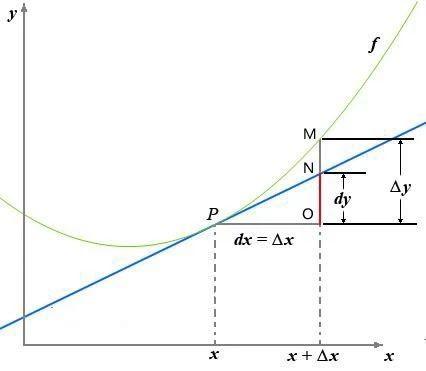
蓝色切线的斜率表示在P点的导数,如果我们继续用dy/dx表示导数的话,那么从图里就可以清楚的看到:dx表示在x轴的变化量,dy就刚好表示蓝色的切线在y轴的变化量。
也就是说,当自变量变化了Δx的时候,Δy表示实际的曲线的变化量,而微分dy则表示这条切线上的变化量,这就是新的语境下函数微分dy的含义。而自变量的微分dx,大家可以看到,就跟x轴的变化量Δx是一回事。
由于切线是一条直线,而直线的斜率是一定的。所以,如果我们假设这条切线的斜率为A,那么dy和Δx之间就存在这样一种线性关系:dy=A·Δx。
这些结论都可以很容易从图中看出来,但是,一个函数在某一点是否有微分是有条件的。我们这里是一条很“光滑”的曲线,所以在P点有微分dy,也就是说它在P点是可微的。但是,如果函数在P点是一个折点,一个尖尖的拐点呢?那就不行了。因为有拐点的话,你在这里根本就作不出切线来了,那还谈什么Δy和dy?
关于函数在一点是否可微是一个比较复杂(相对科普的复杂~)的问题,判断曲线(一元函数)和曲面(二元函数)的可微性条件也不太一样。直观地看,如果它们看起来是“光滑”的,那基本上就是可微的。
微分的严格定义是这样的:对于Δy是否存在着一个关于Δx为线性的无穷小A·Δx(A为常数),使它与Δy的差是较Δx更高阶的无穷小。也就是说,下面这个式子是否成立:
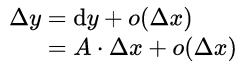
o(Δx)就表示Δx的高阶无穷小,从字面上理解,高阶无穷小就是比无穷小还无穷小。当Δx慢慢趋向于0的时候,o(Δx)能够比Δx以更快的速度趋向于0。比如当Δx减小为原来的1/10的时候,o(Δx)就减小到了原来的1/100,1/1000甚至更多。
如果这个式子成立,我们就说函数y=f(x)在这点是可微的,dy=A·Δx就是函数的微分。因为这是一个线性函数,所以我们说微分dy是Δy的线性主部。
这部分的内容好像确实有点乏味,莱布尼茨时代的微分dy就是一个接近0又不等于0的无穷小量,理解起来非常直观。但是,我们经过ε-δ的极限重新定义的函数的微分dy竟然变成了一个线性主部。这很不直观,定义也挺拗口的,但是这样的微积分才是现代的微积分,才是基础牢固、逻辑严密的微积分。

为了让大家对这个不怎么直观的微分概念也能有一个比较直观的概念,我们再来看一个非常简单的例子。
我们都知道半径为r的圆的面积公式是S=πr²。如果我们让半径增加Δr,那么新的圆的面积就应该写成π(r Δr)²,那么,增加的面积ΔS就应该等于两个圆的面积之差:

大家看到没有,这个式子就跟我们上面的Δy=A·Δx o(Δx)是一模一样的。只不过我们把x和y换成了r和S,A在这里就是2πr,这里的π(Δr)²是关于Δr的平方项,这不就是所谓的高阶(平方是2阶,Δr是1阶,2比1更高阶)无穷小o(Δx)么?
所以,它的微分ds就是2πr·Δr这一项:
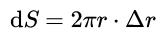
它的几何意义也很清楚:这就是一个长为2πr(这刚好是圆的周长),宽为Δr的矩形的面积,好像是把这个圆“拉直”了所得的矩形的面积。
好了,微分的事情就说到这里,剩下的大家可以自己慢慢去体会。毕竟这是一篇关于微积分的科普文,再写太多就成教材了。
关于微积分的重建,我们已经看到了如何在ε-δ定义的新极限下重新定义了积分和微分,也看到了在这种新的定义下,积分和微分的概念跟以前有什么不同。沿着这条路,我们还能非常严格的证明微积分基本定理,也能很好地处理连续性、可微性、可导性、可积性等问题。虽然在具体的计算方式上跟以前的差别不大,但是微积分的这个逻辑基础已经跟以前发生了翻天覆地的变化,这个差别大家要仔细体会。
在魏尔斯特拉斯给出极限的ε-δ定义之后,微积分的逻辑问题基本上解决了,但还有一些其它的问题。比如,有了微积分,数学家们当然就希望尽可能多的函数是可以求出积分的,但是你像来砸场子的狄利克雷函数(x为有理数的时候值为1,x为无理数的时候值为0)就没法这样求积分。
不信你想想,一个在有理数为1,无理数为0的函数你要怎么去切块?它在任何一个地方都是不连续的,你甚至连它的图像都画不出来,怎么用矩形去逼近?所以,这里就有一个棘手的问题:一个函数到底要满足什么条件才是可以求积分的呢?
这个问题一直拖到20世纪初才由大神勒贝格解决。勒贝格把我们常见的长度、面积概念做了一个扩展,得到了更一般的测度的概念。然后,他基于这种测度定义了适用范围更广的勒贝格积分,于是,原来无法求积分的狄利克雷函数在勒贝格积分下就可以求积分了。然后,勒贝格基于测度的理论也给出了一个函数是否可积的判断条件,完美收官!

于是,我们这段跨越两千多年,从阿基米德到勒贝格的微积分之旅就要告一段落了。
古希腊人和古代中国人都知道用已知的多边形去逼近复杂曲线图形,阿基米德用穷竭法算出了一些简单曲线围成的面积,刘微用正多边形去逼近圆,也就是用割圆术去计算圆周率。
牛顿和莱布尼茨发现了“微分和积分是一对互逆运算”这个惊天大秘密,正式宣告了微积分的诞生。
柯西和魏尔斯特拉斯用ε-δ语言重新定义了极限,把风雨飘摇中的微积分重新建立在坚实的极限理论基础之上,彻底解决了幽灵般的无穷小量的问题,解决了第二次数学危机,也在数学领域解决了芝诺悖论。
勒贝格基于集合论,对积分理论进行了一次革命,建立了定义范围更广的勒贝格积分,并且进一步把这场革命推进到了实分析。
我的文章虽然以勒贝格结尾,但这丝毫不代表微积分在勒贝格这里就走向了完结,即便这时候已经是20世纪初了。

20世纪60年代初,有一个叫鲁滨逊的德国人重新捡起了莱布尼茨的无穷小量。他把实数扩展到非实数,直接把无穷大和无穷小变成了非实数域里的一个元素。所以他的理论可以直接处理无穷小量,这是第一个严格的无穷小理论。
我们知道,幽灵般的无穷小量在微积分建立初期掀起了腥风血雨,后来经过柯西和魏尔斯特拉斯的拼命抢救,才终于在坚实的ε-δ极限理论之上重建了微积分。柯西和魏尔斯特拉斯的这一套让微积分严密化的方法被称为标准分析。
而鲁滨逊认为,无穷小量虽然不严谨,但是大家基于无穷小量做的微积分计算却也都是正确的,这至少表明无穷小量里应该也包含着某种正确性。ε-δ极限是一种绕弯解决无穷小量不严谨的方法,但是这种方法并不是唯一的。鲁滨逊选择直接面对无穷小量,直接建立了另一种让微积分严密化的方法。因此,与柯西和魏尔斯特拉斯的标准分析相对,鲁滨逊的这种方法被称为非标准分析。

提出了不完备定理的数学大神哥德尔就对非标准分析推崇备至,他认为非标准分析将会是未来的数学分析。他说:“在未来的世纪中,将要思量数学史中的一件大事,就是为什么在发明微积分300年后,第一个严格的无限小理论才发展起来。”
我们现在就处在哥德尔说的未来的世纪中,各位看官对这个问题有没有什么看法呢?如果我的这篇文章能够让大家对微积分,对数学感兴趣,进而开始自己独立的思考这些问题,那就善莫大焉了~
此外,我希望长尾科技的这篇文章也能多多少少改变一下大家对数学的看法:数学不等于计算,数学也不等于应用,绝妙而深刻的数学思想(比如发现微分和积分是互逆过程)和严密的逻辑(如使用ε-δ定义极限)反而是更重要的。而且,数学的壮观之美也往往需要站在后面两个角度上才能体会到,我很难相信有人会觉得重复的做计算是很有趣的,这也是很多人不喜欢数学的原因。
但是,我绝对相信那些真正认识了数学的人,他们是发自内心的觉得数学美丽动人。

并不是那些数学大神们很奇怪,而是他们确实看到了常人没能看到的绝美风景。
,




