
第81回
流沙河畔,巍峨烟窗入云端
望江楼上,欲穷千里存疑惑
话说沙僧担心铸造厂的烟窗安危,让八戒算一下此次经过沙河市台风的最大风力是几级?
八戒说,"这个很简单,当市中心A距离台风中心最近时所受的风力最大,也就是说当台风中心在点D时,沙河市所受的风力最大,最大风力为16-150÷20=8.5(级)."
沙僧一听影响沙河市的最高风力将到达到8.5级,立即吩咐工人们对烟窗进行加固。
沙僧亲自出马,八戒紧随其后,兄弟俩加大油门朝铸造厂开去,远远就看到一座熄火已久的大烟窗似乎在风中摇曳.
这是在扩建铸造厂规模后新建一个大型冶炼炉,炉的烟窗是一个高达近百米的大圆柱,圆柱底面周长90米,高为120米。
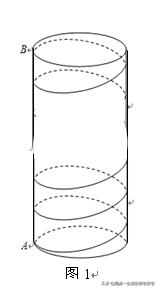
为了抗击这次的台风,沙僧决定从圆柱底端的点A处开始顺着圆柱侧面用一条特制的钢线均匀地绕30圈到圆柱顶端B处,且A、B在同一母线上(如图1)。
"沙总,钢丝线需要购买多长呢?"负责购买钢线的工人问。
"二师兄,你赶快帮我算一下,按照设计钢丝线最少需要多少米?"
"好的,沙师弟。"八戒说,"知道需要多长的钢丝线,首先把圆柱展开成矩形,然后再利用'两点之间,线段最短'可以解决。"
"这个我也知道."沙僧说,"把圆柱沿母线AB展开后所得矩形的底边是圆柱底面的周长90米,高就是圆柱的高120米,可是把矩形对角线的长√(90平方 120平方) =150(米)作为钢线的最短长度好像不对啊?"
"你这个答案确实不对."八戒说,"那是从点A绕一圈到点B的最短长度,而这里要绕的是30圈."
"那是不是需要30×150=4500(米)吗?"沙僧问.

"这也不对."八戒说,"你看如图2,绕30圈时每一圈的长不是150米.注意到绕一圈时,钢线上升的高度只有4米,而不是120米,因此,这种情况下绕一圈的最短长度是√(90平方 4平方) =√8116=2√2029(米),所以绕30圈需要最短钢线长为30×2√2029=60√2029≈2703(米),因此,最少大约需要购买2703米长的钢线."
台风过后,沙僧工厂丝毫未损,沙河市秩序井然,市民们依旧日出而作,日落而休。
第三天,沙僧、八戒带着猪小能来到了沙河市最高酒楼望江楼,这是一家集饮酒和观光于一体的五星级大酒楼,站在酒楼的顶层可以鸟瞰沙河市全貌,由于刚经过台风的洗礼,空气格外清新,天空格外晴朗,眺眼远处山峦叠嶂,云蒸雾绕,流沙河水一望无际,犹如天上而来。
沙僧忽然想起了王之涣"欲穷千里目,更上一层楼"的诗句,他遂向八戒问道:"二师兄,你说再上一层楼究竟能多看多远呢?"
"这个我可没想过。"八戒说,"不过我们可以算算看的。"
"这个也能算吗太爷爷?"小能觉得奇怪,"怎么算呢?"

"把地球看成是球体,它的半径R=6 400 000米,如图3是经过圆心的截面。"八戒说,"假设我们现在所在的位置点A与地球表面的点B的距离为h米,则AB经过圆心O,此时能看到地球表面上的最远点为C,则AC是圆O的切线,连接OC,则OC⊥AC.
在Rt△OAC中,OA=R h,OC=R,由勾股定理,得
AC=√[(R h)2-R2] =√(h2 2Rh).
当h=100时,这差不多是这栋楼的高度吧?"
"这栋楼地平面上有33层,差不多100米高没错的。"沙僧肯定地说。
"当h=100时,我们的视线长度是
AC=√(100平方 2×6400000×100)
=√1280010000≈35777(米)
当我们再上一层楼时,高度增加了3米,此时h=103,
AC=√(103平方 2×6400000×103)
=√1318410609≈36309(米),
原来可以看到的最远距离是35777米,
再上一层楼后可以看到的最远距离是36309米,
36309-35777=532(米),
因此,更上一层楼只能多看500多米远."
"原来'欲穷千里目,更上一层楼'是骗人的名句啊!"沙僧叹道。
"太爷爷,如果想真的看到千里之外,需要站在多高的位置呢?"
"古时的一千里是500公里,也就是500 000米,"八戒说,"在图3的Rt△OAC中,OA=R h,OC=R,AC=500 000,由勾股定理,得
R h=√(R2 500000平方)
=√(6400000平方 500000平方) =6419501,
所以h=6419501-R=6419501-6400000=19501(米).
这就是说,要想看到千里之外,除了需要高倍的望远镜外,还需要在约20千米高的空中才能看得到.
看来'欲穷千里目','更上一层楼'是远远不够的。如果每层楼高3米,需要站在6千楼顶上才能看到千里之外啊!"
望江楼的江老板和沙僧是故交,他知道沙僧跟他二师兄八戒一起来后特意出来跟八戒打招呼,并吩咐备办酒宴热情招待。

席间,桌上放着一包如图4打开的香烟,八戒拿起来仔细一看,包装盒的横截面是如图5的矩形ABCD,20支香烟的排列横截面是20个相同的小圆,上下左右相邻的两圆外切(两圆有唯一的公共点且除这个公共点(切点)外圆上的其他各点都在另一个圆上),每支香烟底面圆的直径都是8mm.

"小能,你能算出制作这种香烟的包装盒的横截面矩形ABCD的面积是多少吗?"
"矩形ABCD的长AB是7个圆直径的和=7×8=56(mm)。"小能说,"高AD是多少我算不出来。"
"我告诉你,如果两圆外切,圆心的距离等于两圆半径的和。"八戒说,"在如图5中,选择⊙O1、⊙O2、⊙O3,连接这三个圆心,得等边三角形O1O2O3,你说这个△O1O2O3的边长是多少?"
"是4 8 4=16(mm)。"小能说,"我知道怎么做了。先求等边△O1O2O3的高,再加上两个圆的半径就是矩形ABCD的高。"
"是的。"八戒说,"你再算一下。"
"在等边△O1 O2 O3中,作底边O2O3上的高O1 E.
则在Rt△O1O2E中,O1O2=16,O2E=8,
所以O1E=√(16平方-8平方) =8√3≈13.84.
∴ AD=O1E 8=13.84 8≈21.8(mm).
所以矩形ABCD的面积
S=AB·AD=56×21.8=1220.8(平方毫米),
约为12.2平方厘米。"
猪小能刚算完香烟包装盒截面积后,服务员开始来上饭菜。大家静下来吃饭。

吃饱饭后八戒、沙僧和江老板开始喝酒,小能则自个儿在包厢角落里一个玩儿童玩具。他在点A处推出一个圆形的大"硬币",让它沿着如图6的点A→B→C→D的路线滚动,然后掉入凹槽中。
前几次试玩时,"硬币"总是滚不到凹槽里就倒下了,后来终于成功了。玩腻了后,小能认真观察后发现:"硬币"的直径为60cm,AB=300cm,BC=400cm,CD=500cm,∠ABC=∠BCD=150°。然后思考着这样一个问题:
"硬币"从点A滚动到点D,在这个滚动观察中"硬币"的圆心O经过的路程是多少呢?"
小能想了好久也没算出来,他跑过来问八戒。八戒说:
"要想知道圆O从点A滚到点D圆心O经过的路程,需要先知道在这个过程中圆心O经过的路线。你知道这条路线吗?"
"是不是一条与折线AB→BC→CD平行的折线?"小能不敢确定。
"不全是。"八戒说,"圆O在AB这段路上滚动时,圆心O经过的路线是与AB平行且相等的线段没错,但圆O从AB路段改为在BC路段,此时圆心O要经过一次旋转;在BC路上滚动时,圆心O经过的路线与BC平行,但路程与BC是不相等的;在CD上滚动时,圆心O经过的路线与CD平行,但路程与CD也是不相等的;同样地,在CD上滚动时,圆心O经过的路程与CD也是不相等的。"
"为什么不相等呢?"

"因为圆O从BC路段上滚动改变为在CD路段上滚动,圆不需要经过点C。"八戒说,"圆心O滚动的路线如图7所示,其中弧O1O2是圆O从AB路段变为BC路段这个过程经过的路线,点E是圆O在BC上最后一个点,点F是圆O在CD上的起点。"
"我知道了,圆心O经过的路线长是OO1 弧O1O2 O2O3 O3O4。其中OO1=AB=300。"小能问,"可是如何求其他段的长呢?"
"想求弧O1O2的长必须知道圆的半径及弧的度数,其中半径是30cm,你能算出弧O1O2的度数吗?"
"∠O1BO2=360°-∠ABO1-∠ABC-∠ CBO2
=360°-90°-150°-90°=30°,
所以弧O1O2的长=30л×30/180=5л (cm).
如何求O2O3和O3O4的长呢?"
"O2O3=400-CE,O3O4=500-CF。"八戒说,"由切线长定理,CE=CF,先求CF的长。"
"可是如何求CF的长呢?"

"这的确是个难题。"八戒喝完杯中酒后说,"我们把四边形ECFO3分离出来并放大为图8,延长FC与O3E的延长线交于点G。由已知,O3E=O3F=30cm,∠ECF=150°,∠O3EC=∠F=90°,所以∠O3=30°,
所以∠G=60°。
设EG=xcm,则CG=2x,CF=CE=√3x,
所以GF=2x √3x,O3G=x 30,
由O3G=2GF,得
x 30=2(2x √3x),
整理,得(3 √3)x=30,x=30/(3 √3) =15-5√3,
所以CE=CF=√3x=√3(15-5√3)=15√3-15,
所以O2O3=400-CE=400-(15√3-15)=415-15√3,
O3O4=500-CF=500-(15√3-15)=515-15√3,
所以圆心O经过的路线长OO1 弧O1O2 O2O3 O3O4
=300 5л 415-15√3 515-15√3
=1230 5л-30√3
≈1193.7(cm)。"
正当八戒爷孙俩聚精会神进行计算时,沙僧的微信提示声突然响了起来。
欲知谁发来的微信?请看下回分解。
,




