多少人被数学深深折磨着,他们只知道学数学的痛苦,却不知道数学也有浪漫的一面。
如果一个自然数的所有正约数(除去它本身)之和等于另一个数,并且反过来也对。那么,这两个数便称为"亲和数"。
如284和220使是一对亲和数。请你找出2620的亲和数。
先来验证一下284和220是一对亲和数。将284和220分别写成质因数的乘积。因为
284=2×2×71,故所有正约数有1,2,2×2=4,71,2×71=142,因此,
1 2 4 71 142=220。
220=2×2×5×11。
所有正约数有1,2,4,5,10,11,20,22。44,55,110。因此。
1 2 4 5 10 11 20 22 44 55 110=284。

这一对最奇妙的数字,就好像一对情侣把自己的心一片片分解并献给心爱的对方。两个数字彼此相互渗透、相互包容,就像两个相爱的人共同演绎一段美好的爱情。据说中世纪曾流行这种成对的护身符,一个刻着220,一个刻着284,用于恋人们祈求爱情的忠贞。

利用同样的方法,因为2620=2×2×5×131,故有
1 2 5 131 4 10 262 655 20 1310 524=2924;2924=2×2×17×43所以1 2 17 43 4 34 86 68 172 34×43 731=2620。
因此2620的亲和数是2924。
并非任何一个自然数都有亲和数。例如。由24=2×2×2×3。
得1 2 3 4 6 8 12=36;而由36=2×2×3×3。
得1 2 3 4 6 9 12 18=55/24。因此,24无亲和数。

亲和数是属于数论研究的范畴。西方人认为,在数论发展过程中最初迈出振奋人心的几步的是毕达哥拉斯及其继承人。
例如,在大约公元320年,有影响的柏拉图派哲学家伊安布利霍斯(lamblichus)把亲和数的发现归功于毕达哥拉斯。
据说,220和248这对亲和数是由毕达哥拉斯发现的,是人类认识的第一对亲和数,也是最小的一对亲和数。
古希腊数学家毕达哥拉斯的一个门徒向他提出这样一个问题:"我结交朋友时,存在着数的作用吗?"毕达哥拉斯毫不犹豫地回答:"朋友是你的灵魂的倩影,要像220和284一样亲密。"又说"什么叫朋友?就像这两个数,一个是你,另一个是我。"
古代欧洲人十分推崇亲和数,甚至赋予一种神秘色彩,他们相信写着220和284的两块符咒可以确保佩戴人亲密无间;他们相信吃下刻有220和284的两个水果能促进爱情。就连《圣经》中也有记载,《创世纪》(32:14)中,雅各布把220头羊当礼物送给孪生兄弟以扫,神学家们认为山羊的数目220(一对亲和数中的一个)表达了雅各布对以扫的友爱之情。

这两个数字在占星术中起着重要作用,相传在远古时期,人类的一些部落把这两个数字奉若神明。男女青年结束婚姻时,往往把这两个数分别写在不同的标签上,两个青年在抽签时,若分别抽到这两个数,便结为终身伴侣;若抽不到,则因天生无缘,便分道扬镳了,因此,也把此对数称为相亲数。对唯物主义者,送给情人一块符咒可以视为一种乐趣。
在发现最初的一对亲和数284和220以后,很长一个时期内没有发现新的亲和数。直到公元9世纪才稍有进展。公元850年,伊拉克数学家塔比特·伊本·库拉在《亲和数的确定》一文中,给出一个求亲和数的法则,被称为塔比特法则。

由于要判断p、q、r是不是素数,尤其当n较大时,运算繁杂,操作困难,在当时并没有帮助人们找到第二对亲和数。
其实该法则,只有当n=2,4,7时,能产生3对亲和数。在n=7之后再也不能产生其他亲和数对。

9世纪之后的几百年内关于亲和数的研究依然进展甚微。1636年,伟大的法国数论学家费马(Fermat,1601-1665)才发现第二对17296和18416。

1747年-1750年间,瑞士数学家欧拉先是找到30对亲和数,后来又扩展到60对。欧拉不仅列出了亲和数的数表,而且还公布了全部运算过程。欧拉将亲和数分为五类加以讨论。例如第一类是寻找形如(apq,ar)的亲和数对,欧拉分别讨论了a的各种取值情况,最后他在第一类中就找到了11对亲和数。
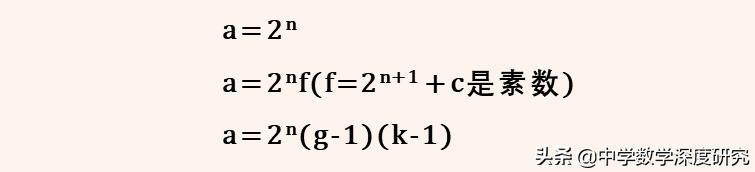
欧拉改进了实用性不强的塔比特法则,形成欧拉 法则。

然而通过欧拉法则能找到的亲和数仅有五对。(m,n)分别为(1,2)、(3,4)、(6,7)、(1,8)、(29,40)。当n<2500时,再也找不到其他的亲和数。可见,欧拉法则并不是寻找亲和数的万能公式。

在寻找亲和数的过程中有一个趣闻:长期被忽略的、相当小的一对亲和数1184和1210,是直到1866年才由年仅16岁的意大利少年帕加尼尼(Paganini)发现,令数学家如痴如醉,到1974年,人们知道的一对最大亲和数各有152位:

亲和数的概念在现代又有了新的推广。例如,由三个或三个以上的数组成的一个循环序列,如果其中任何一个数的真因子之和都等于下一个数,则称为亲和数链.现在仅仅知道两个由1000000以下的数组成的亲和数链,其中一个是由12496开始,有五个"环",由波利特(Poulet)发现;另一个由14316开始,有28个"环"。
也还知道某些由1000000以上的数组成的四链亲和数链.恰好有三个"环"的亲和数链称为"伙"(Crowd),目前尚未发现"伙。

从公元前5世纪到今天,数学家从来没有停止寻找亲和数的脚步,对亲和数的研究不断深入。尽管如此,亲和数还有不少未解之谜。
1.亲和数是否有无穷多个?有没有通用的法则来构造亲和数?
2.目前找到的每一对亲和数所含的两个数都同为偶数或同为奇数,是否存在一对亲和数是一奇一偶?
计算机的问世使寻找亲和数变得简单明了了,但是,即使是计算机也没有突破长久以来的局限,在未来的漫长旅途中我们的数学家会不会给我们带来惊喜呢?让我们拭目以待吧。
,




