tag:这篇文章没太多思考的地方,就是做个过渡
1.从条件概率来定义互斥和对立事件
2.互斥事件是独立事件吗?
3.每个样本点都可以看作是互斥事件,来重新看待条件概率
一、从条件概率来定义互斥和对立事件
根据古典概率-条件概率的定义,当在“A的样本点集合中,没有一个B集合中的样本点”的时候:
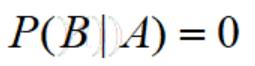
则A、B事件构成了一对互斥事件,简单理解就是发生了A就绝对不可能发生B,又根据条件概率的展开式,我们可以推出常见的两个公式:

互斥事件在V-N图上来看,就是两个事件的集合没有交集。

二.互斥事件是独立事件吗?
互斥事件不仅不是独立事件,还是一种关系十分紧密的事件,它的关系是“如果A发生,则B一定不发生”,这是可谓是你死我活般的关系。
独立事件的意思是“A的发生对B的发生概率值没有任何影响”,这不仅仅有影响还给全面否定了。
三.每个样本点都可以看作是互斥事件,来重新看待条件概率
因为每个样本点之间都是没有任何交集的,所以各个样本点之间都是互斥事件。
(1)A事件的发生=A集合中的任意一个样本点发生。
(2)由互斥事件含义,A集合外的任意一个样本点都不可能发生。
(3)在条件A的约束下,我们不可能选择到A集合外的样本点。
(4)也就是说我们只能从A集合中任意选择一个点
(5)如果选择的是样本点也在B集合中,那么就是P(B|A)
由此我们推出从互斥事件的角度来理解的条件概率的公式:






