{1,2,3,4···}和{2,4,6,8···}谁比较大?
这是一组无穷数列之间的比较。凭直觉来看,那肯定是前者大!因为正整数不仅包含着偶数,还包含着奇数呢。但是这么想是错的。那要怎样比较一组无穷数列呢?
我们可以从非洲的土著人们学习最原始的方法。一位土著人想要清点自己的财产,看看是玻璃珠更多还是铜币更多。可是土著人没有数学知识,他最多只能数1,2,3。3已经是他认知范围内的最大数字了。于是土著人想到,把玻璃珠和铜币拿出来一一地比较:在一颗玻璃珠旁边放上一枚铜币,然后在第二颗玻璃珠旁边放上第二枚铜币,以此类推······如果玻璃珠摆完了而铜币还有剩余,那么就是铜币更多。如果铜币摆完了而玻璃珠还有剩余,那么就是玻璃珠更多。这就是这就是“无穷数学奠基人”康托尔提出的比较无穷数列的方法:一一配对法:即每个集合分别与另一个集合里的元素相对应,如果他们正好一一对应,那么这两个集合相等。如果某个集合中存在无法配对的剩余元素,那么可以说这个无穷数更大。
那么我们该如何比较{1,2,3,4...}和{2,4,6,8...}呢?如下图所示,我们将{1,2,3,4···}里的元素与{2,4,6,8···}里的元素配对,发现它们是可以一一对应的。或许你会提出疑问,为什么偶数里的2,4等不是对应整数里的2,4等呢?我是这么理解的:比较无穷数列,要把集合里的元素想成只是一样东西,这个元素它独特的样子和性质与我们要比较这集合里有多元素无关。像土著人一样,拿出这堆铜币里的一个,和拿出这堆玻璃珠里的一个,一一配对即可;拿出这个集合中的一个元素,它就只是代表这个集合中的一个元素,与另一个集合中的一个元素配对,看看谁配完了还有剩余。因此,我们可以得出,{1,2,3,4...}和{2,4,6,8...}是相等的。

配对法
呃,或许你会说,那这样比较的话是不是所有的无穷数列都相等。如果这样的话那比较这些数有什么意义呢?不是的,就比如一条线上的点就比整数和分数大。首先我们需要知道,整数和分数是一样大的。我们可以先写下分子与分母和为2的分数:1/1;接下来是分子分母和为3的2/1,1/2···依次类推写下和为4的,和为5的······我们会发现这个数列中的每一项和分数数列一一对应,即分数的数量和整数的数量相等。所以回到上面的问题,我们知道每个分数都可以化作一个有限小数或者一个无限循环小数,而点的位置对应可以是无限不循环小数。因此一条线上的点和整数或分数之间无法建立一一对应的关系。所以说,一条线上的数量大于整数或分数的数量。
用这种一一配对法,我们还可以比较线,面,和立方体内所有几何点的数量,得出它们是相等的。而所有种类的几何曲线的数量大于前者的数量。
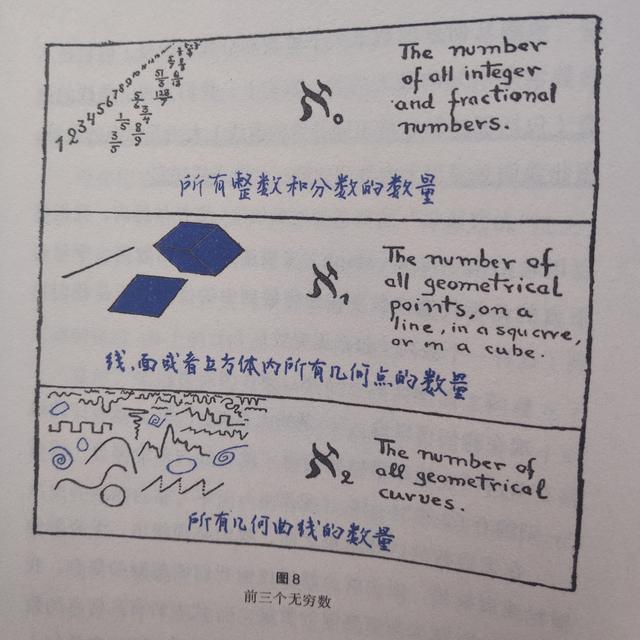
《从一到无穷大中》的插图
这是我在《从一到无穷大》中学到的内容。本书作者乔治·伽莫夫搜集现代科学中最有趣的事实和理论,先从最简单的记数开始,讨论古人如何记大数字,无穷大有多大,复数有什么作用等这些问题。紧跟着作者开始讲述拓扑,怎样理解四维时空,用精妙的语言阐述爱因斯坦的相对论,时空弯曲到底是什么。再后来伽莫夫会带着我们走进微观世界,讲述分子,原子和原子核,并顺带讲述基因与遗传。在最后一部分伽莫夫谈到了自己最擅长的领域——宇宙学,用自己创立的理论——宇宙大爆炸理论(没错,这个理论就是伽莫夫创立的)解释宇宙是如何产生的,还有太阳为什么会发光,宇宙到底有多大,宇宙多少岁等问题。全书只有二十多万字,却可以让我们了解到现代科学的基本全貌,以通俗易懂,充满趣味的语言带领读者徜徉在科学的殿堂中,感受科学的魅力。这本书被列为“20世纪最伟大的科普著作”,成为许多现代科学家的启迪读物。笔者看完这本书后,受益匪浅,感觉发现了新世界的大门,让我们看似深不可测,固涩难懂的现代科学竟然这么有魅力。所以向小伙伴们安利这本书,说不定这本书能激起你对数学物理生物的兴趣,然后凭着一股儿热劲努力学习,发现自己可能有科学家的天赋,突然想到了什么奇思妙想的点子,成为了一名科学家,推动了人类科学的进步······

书里还会夹有两张思维导图
,




