1有理数
(1)有理数的定义:正整数0负整数统称为整数:正分数、负分数统称为分数.整数和分数统称为有理数.
(2)有理数的分类

2数轴
(1)数轴的定义
在数学中,可以用一条直线上的点表示数,这条直线叫做数轴,它满足以下要求:
1.在直线上任取一个点表示数0,这个点叫做原点;
2.通常规定直线上从原点向右为正方向,从原点向左为负方向;
3.选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表1,2,3,……从原点向左,用类似方法依次表示-1,-2,-3,……
分数或小数也可以用数轴上的点表示,如图所示.
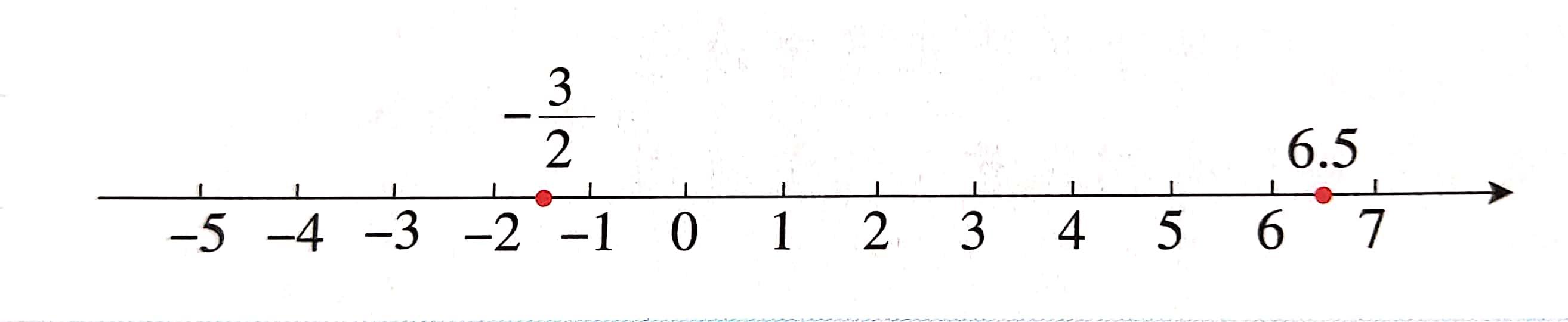
(2)数轴上的点和有理数
一般地,设a是一个正数,则数轴上表示数a的点在原点的右边,与原点的距离是a个单位长度;表示数-a的点在原点的左边,与原点的距离是a个单位长度.
3相反数
(1)相反数的概念
像3和-3,4和-4这样,只有符号不同的两个数叫做互为相反数.
一般地,a和-a互为相反数,特别地,0的相反数是0.这里,a表示任意一个数,可以是正数、负数,也可以是0.
(2)几何意义
互为相反数的两个数在数轴上对应的两个点位于原点的两侧且到原点的距离相等;反之,位于原点的两侧且到原点的距离相等的点所表
示的两个数互为相反数.
(3)相反数的性质
任何一个数都有相反数,而且只有一个.正数的相反数一定是负数;负数的相反数一定是正数;0的相反数仍是0.
4绝对值
(1)绝对值的定义
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|al.
(2)绝对值的意义
1.绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
即 如果a>0,那么|a|=a;
如果a=0,那么|a|=0;
如果a<0,那么|a|=-a.
2.绝对值的几何意义:一个数的绝对值就是表示这个数的点到原点的距离,离原点的距离越远,绝对值越大;离原点的距离越近,绝对值越小.
(3)绝对值的性质:绝对值具有非负性,即有|a|≥0;若几个数的绝对值的和为0,则每个数都等于0,即|a| |b| ... |m|=0,则a=b=...=m=0.
5有理数大小的比较
在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,
即左边的数小于右边的数.从而可知:
正数大于0,0大于负数,正数大于负数;
两个负数,绝对值大的反而小.

使用思维导图:(建议保存打印思维导图)
知识盘点:所学知识点通过大脑首尾因效应,每天晚上复盘知识点,第二天早上再复盘,持续维持记忆高峰。思维导图比翻书有趣也更快。
查漏补缺:复习知识点时,遇到不熟悉的不会的不理解的知识点在思维导图中标注符号△,找老师解决知识点问题,重点复习。
错题处理:遇到错题,分析错题,分析自己错的根源在哪里,找出来错的知识点,在思维导图进行标注★,每错一次标注一次,有可能同一个知识点会标注多次。再进行复习时,明确知道自己的误区盲区在哪里,自己的失分点在哪里,解决了,分数就上来了。
热爱思维导图,擅长思维导图,愿与你分享所有与思维导图有关的一切!文章来源:公众号贱贱的贱老师
,




