自从上一次出版到现在已经有一段时间了。但是其间,三次重要的会议让我远离了博客。我对自己说,针对我说过的题目,我必须写博客,但是我根本没有机会。
现在,离JavaOne发布还比较遥远,而且我已完成我的新书 《JavaFX8,Introduction by Example》,该书与我的朋友Carl Dea, Gerrit Grunwald, Mark Heckler and Sean Phillips共同编写完成,很快就会印刷出版。我有机会使用Java 8和JavaFX 3D几个星期,这篇文章就是我探索的结果。
很偶然我的孩子最近在家摆弄魔方,为了感谢源自David Gilday的这个令人惊讶的项目,我们建立一个乐高头脑风暴EV3处理机器人,David Gilday在CubeStormer3中最快复原了魔方,EV3见下图。

图一
在我玩魔方一段时间后,我在考虑创建JavaFX应用程序解决魔方难题的可行性,以及RubikFX如何诞生的问题。如果你急切地想了解RubikFX是怎么一回事,以下YouTube上的视频将向你展示大部分内容。https://www.youtube.com/watch?v=ZVPIBkDgZV4
总体上讲,在这篇文章中我将讨论在一个Scene中导入3D模型,使用放大、旋转、缩放的功能,加入光线,移动摄像头等等。一旦我们有一个非常好的3D魔方模型,我们将努力找到一种独立于模型剩下的部分方式,移动模型层块,保留变化的轨迹。最后,我们将加入通过鼠标点击,选择面、转动层块。
如果你不熟悉魔方的概念和复原它的基本步骤,请阅读以下内容。
在我们开始以前
你也许知道Java8已经在3月18日发布了,所以本项目的代码是基于这个版本的。如果你还没有Java8,请下载新的SDK更新你的系统。我采用NetBeans8.0开发本项目,它支持lambdas表达式和新的Stream API。你可以从以下链接更新你的IDE。地址:https://netbeans.org/downloads/
我使用了2个独立的构件,一个用来导入模型,它是OpenJFX项目的一部分,来源于一个实验性的项目3DViewer。我们需要下载和编译它。另一个来源于ControlsFX项目,它可以为应用程序添加酷炫的对话框。
下载地址:http://fxexperience.com/downloads/controlsfx-8.0.5.zip
最后,我们的项目需要一个3D模型,你可以自己建立一个或者使用一个免费的,你可以从下面的地址下载,采用3ds或者OBJ的格式下载。
地址如下:
http://tf3dm.com/3d-model/rubik39s-Cube-79189.html
(原作者提供的下载地址,据我尝试,该文件不能下载了。但是完整版的资源文件中,已经有这个3D模型了)
一旦你得到所有的组件,你可以很容易地得到这张图片。
用3DViewer程序打开3D模型
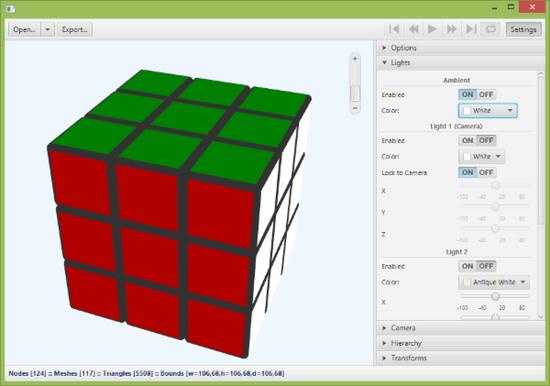
图二
解压文件,将‘Rubik's Cube.mtl'重命名为‘Cube.mtl',将'Rubik's Cube.obj'重命名为'Cube.obj',编辑该文件将第三行改为‘mtllib Cube.mtl',(用文本编辑器打开)然后保存。运行3DViewer应用程序,将'Cube.obj'拖到viewer中。打开设置面板,选择灯光,打开白色环境光源,关掉puntual(好像是拼错了)光源。你可以放大或者缩小(使用鼠标滚轮、右击、导航条)。旋转魔方用左键(编辑旋转速度用CTRL或者SHIFT),或者用鼠标按键全部按下。
选择Options面板,点击Wireframe,你可以看到建造模型的三角面块。

图三
27个立方体中的每一个都在OBJ文件中给予了一个名称,类似‘Block46’等。所有的三角面块都被集合在一起,且赋予了材质,每个立方体由1到6个面块组成,名字类似‘Block46', ‘Block46 (2)',总共有117个面块。
The color of each cubie meshes is asigned in the 'Cube.mtl' file with the Kd constant relative to the diffuse color.
每个面块的颜色都包含在'Cube.mtl'文件中,漫反射颜色也包含其中。
魔方—精简版
输入3D模型
当我们了解了我们的模型是怎么回事,我们就需要为面块(MeshView)建造节点了(Node)了。3DViewer中的ObjImporter类提供了getMeshes()方法,返回每个面块的名字。我们定义一个HashMap为每个MeshView绑定一个名字,针对每个面块的名字,我们用bulidMeshView(s)方法得到一个MeshView对象。
在设计时,模型中立方体的材质并不反射光线,我们修改它,允许它和Puntual光线交互,通过定义它为Phongmaterial类,编辑材质的特殊粒子属性。
最后,我们将旋转初始魔方,让白色面朝上,蓝色面朝前。
public class Model3D {
/* Cube.obj contains 117 meshes, marked as "Block46",...,"Block72 (6)" in this set:
Cube.obj包含117个mesh面,标识为“Block46”、“Block72 (6)”
*/
private Set<String> meshes;
/* HashMap to store a MeshView of each mesh with its key */
/*哈希表用键值对存储MeshView*/
private final Map<String,Meshview> mapMeshes=new HashMap<>();
public void importObj(){
try {// cube.obj
ObjImporter reader = new ObjImporter(getClass().getResource("Cube.obj").toExternalForm());
meshes=reader.getMeshes(); // set with the names of 117 meshes
//得到117mesh面
Affine affineIni=new Affine();
affineIni.prepend(new Rotate(-90, Rotate.X_AXIS));
affineIni.prepend(new Rotate(90, Rotate.Z_AXIS));
meshes.stream().forEach(s-> {
MeshView cubiePart = reader.buildMeshView(s);
// every part of the cubie is transformed with both rotations:
//魔方的每个部分都要一起变化
cubiePart.getTransforms().add(affineIni);
// since the model has Ns=0 it doesn't reflect light, so we change it to 1
//当NS=0,它不反射光线,我们将它置为1
PhongMaterial material = (PhongMaterial) cubiePart.getMaterial();
material.setSpecularPower(1);
cubiePart.setMaterial(material);
// finally, add the name of the part and the cubie part to the hashMap:
//最后,将魔方每一部份的名字加入hashMap中。
mapMeshes.put(s,cubiePart);
});
} catch (IOException e) {
System.out.println("Error loading model " e.toString());
}
}
public Map<String, MeshView> getMapMeshes() {
return mapMeshes;
}
}
模型导入后自身是白色面朝右(X轴)红色面朝前(Z轴),这就要求2次旋转。
第一次绕X轴旋转-90度,把蓝色面置前,然后绕Z轴旋转90度把白色面置顶。
(魔方的初始状态是白色面朝上,蓝色面朝前)
数学计算上(矩阵运算),第二次绕Z轴旋转的矩阵必须在左边乘以第一次绕X轴旋转的矩阵。但是按照如下情况,如果我们使用add或者append方法在右侧操作,将产生错误。
链接地址:http://hg.openjdk.java.net/openjfx/8/master/rt/file/f89b7dc932af/modules/graphics/src/main/java/javafx/scene/transform/Affine.java
cubiePart.getTransforms().addAll(new Rotate(-90, Rotate.X_AXIS),new Rotate(90, Rotate.Z_AXIS));
cubiePart.getTransforms().addAll(new Rotate(90, Rotate.Z_AXIS),new Rotate(-90, Rotate.X_AXIS));
如果我们先在Z轴旋转,然后在X轴旋转,把红色面置顶黄色面置前,也会产生错误。
尽管进行右侧旋转,将需要次数更多地旋转,使魔方恢复到初始状态,这也比旋转脱离最后状态更加复杂。
所以prepend是正确可行的方法,我们需要采取把最后一次旋转的矩阵记录到Affine矩阵中,而且Affine矩阵中记录所有之前的旋转状态。
,




