导数应用往往是高考数学中的压轴题。其中,求参数的取值范围就是导数压轴题中的难点问题。
一般情况下,求参数的取值范围用“分离参数”这种方法,就能够解决大部分题目。
但是对于剩下的一部分题,在高中阶段,用分离参数的方法却不能顺利解决。
如果想顺畅解决这种类型的题,那么往往只能够进行分类讨论和假设反证。就是根据题干的条件来去对参数进行分类讨论,或者假设出一个具体的数值来去进行反证。
但是在使用分类讨论和假设反证的时候,你要有理有据,并且要能够把具体的数值给反证出来,解题过程往往讨论多样、过于繁杂。
那能不能用一种比较快速的方法来去解决这类问题呢?
答案是肯定有的。
用“洛必达法则”就能够很好的解决这类问题。
因为利用分离参数的方法不能解决这部分问题的原因是,在求导的过程中,会出现“零比零”型(0/0)的式子。而这种形式的数学表达式,是在大学里面去学习的。
那么现在将大学的知识往下放一放,运用到高考数学解题中,就会让繁杂的高考题变得简单可爱起来。
一、什么是洛必达法则?
洛必达法则(l'Hôpital's rule)是利用导数来计算具有不定型的极限的方法,简单来说就是求一个分式的分子和分母都趋于零时的极限的法则。这个法则是瑞士数学家约翰·伯努利(Johann Bernoulli)所发现的。
虽然是由伯努利所发现的,但是当时洛必达花钱将伯努利的这个发现买了下来,所以后人误以为是他的发明,故「洛必达法则」之名沿用至今。
与此同时,洛必达法则也被叫作伯努利法则(Bernoulli's rule)。
好了闲话少说,我们来看具体的应用吧。
洛必达法则的表示方法:




当不满足三个前提条件时,就不能用洛必达法则,这时称洛必达法则不适用,应从另外途径求极限。
(4)若条件符合,洛必达法则可连续多次使用,直到求出极限为止。
也就是说,如果在高中阶段,遇到了求解不定式问题的题目,那么解决这类问题的有效方法就是洛必达法则.
附录知识点:邻域。
邻域是无限小概念会用到的, 即可以无限地接近的一个范围。强调的内容是可以无限小,是一个范围。
去心邻域指的是邻域内不包括某一个点 。
举个例来说,求0 的邻域是可以包括 0在内 的。但是求 0 的去心邻域是,是不包括 0 的在内的。

去心邻域
点a的δ邻域去掉中心a后,称为点a的去心δ邻域。有时把开区间(a—δ, a)称为a的左δ邻域,把开区间(a, a δ)称为a的右δ邻域。
二、例题详解展示


注:分三种情况讨论:

而用洛必达法则就很容易解决这个问题。
下面用洛必达法则来求解:

所以,此时我们 注意到分界点在x=1上。
由洛必达法则有:

关于洛必达法则的运用,我们来继续看几个题目的解题过程,通过分析这些题目的求解过程,记住这些题目的特点,就是当出现了“函数式无意义”的情况时,那么这个时候我们比葫芦画瓢,那么就很容易掌握这种方法。




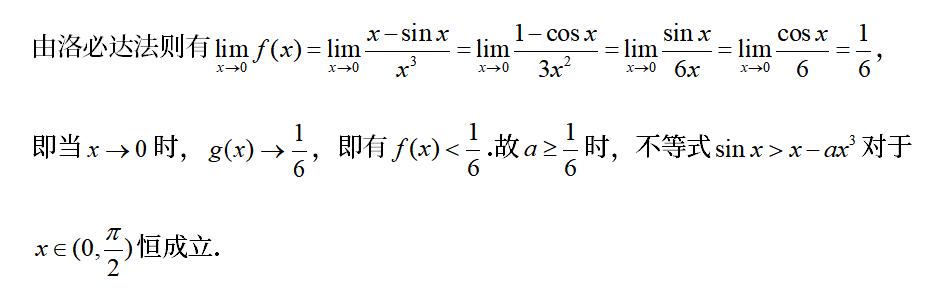
通过以上例题的分析,我们很容易发现应用洛必达法则解决的试题应满足:
(1)可以分离变量;
(2)用导数可以确定分离变量后,所得到的新函数的单调性;
(3)出现“零比零(0/0)”型式子
在解题的过程中,只要出现了上面的形式,那么就可以直接用“洛必达法则”来求解问题。






总结:以上便是高中数学中,用洛必达法则求解不定式的题型展示。在高考过程中,如果遇到以下情形,那么就应该积极的使用洛必达法则来快速解题,以便快速拿到分数。
在函数、导数或数列综合应用的压轴大题中,如果遇到求参数范围的题目,那么在解题的过程中,如果发现会出现“函数式无意义”的情况,如求导的时候,发现表达式的分母为0(即出现“零比零”型式子),或者定义域内的表达式会出现无穷大、无穷小的情况,那么就可以使用洛必达法则。
解题步骤如下:
(1)首先根据题干条件,来逐步的分离变量,把变量单独分离出来,并得到一个全新的函数表达式;
(2)用导数对全新的函数表达式进行求导,在求导的过程中,可以使用二次求导、三次求导或四次求导等,一直求导到最简形式。这个时候,就能够确定新函数的单调性;
(3)确定新函数的单调性以后,再根据相应的定义域,把新函数的取值范围给确定。此时就能够完美的解决这道题目。
(4)需要注意的是,在具体求解的时候,需要看清楚,相应定义域的范围、是大于还是等于、是不小于还是不大于等情况。
同时,有条件,还需要进行验证。这样最终的答案才是最正确的。
三、科普小知识:关于“洛必达法则”诞生的故事
在这篇文章的开篇,我们提到,“洛必达法则”是伯努利所发现的。但是为什么我们耳熟能详的法则名字叫“洛必达法则”呢?
这是因为伯努利在发现“洛必达法则”以后,将这个法则“卖”给了自己的学生——法国贵族王子洛必达。
洛必达,是当时中世纪法国的王公贵族,家庭富有。洛必达非常酷爱数学,他写了很多关于数学的书籍,最有名最重要的著作是《阐明曲线的无穷小于分析》(1696),这本书是世界上第一本系统的阐释微积分学科的教科书,后来这本书在洛必达死后,于1720年在巴黎出版,名为《圆锥曲线分析论》。
在这本书的第九章中,便记载着伯努利所发现的这个法则。而这个法则,就是伯努利告诉洛必达的。
同时,洛必达是伯努利的学生。
前面说了,洛必达这个王子非常酷爱数学,而伯努利又是当时欧洲非常著名的数学家,所以洛必达便拜他为师,跟着天才数学家伯努利研究数学。
当时的约翰·伯努利在生活上遇到了经济上的困境,急需要一笔钱来维持生活,解决现实问题。而他的学生洛必达是一个非常富有的王子,于是洛必达向老师伯努利表示愿意用财物换取他的学术论文。
此时的伯努利也欣然接受。
就这样,在后来影响数学界的“洛必达法则”便富有戏剧性的诞生了。
在洛必达死后,伯努利对外宣称“洛必达法则”是自己的研究成果。但是这个宣称在没有被欧洲的数学家所认可。因为他们认为洛必达的行为是正常的物物交换,因此否认了伯努利的说法。
但无论如何,洛必达和伯努利都是但是最顶尖的天才数学家之一,虽然和老师伯努利比起来,洛必达稍逊一筹,但是不可否认的是,洛必达也确实是个有天分的数学研究者。
在洛必达短短的四十年生命当中(1661-1704),他花费了大量的时间、精力、财力等,来去孜孜不倦的整理这些买来的和自己研究出来的成果,并在1696年写完《阐明曲线的无穷小于分析》这本书的手稿,同时,洛必达还写作过几何、代数及力学方面的文章。
他尽自己的天才所能,极大的传播了数学等科学学科。
更为重要的是,洛必达也是一个谦逊的人,他在此书的前言中,郑重致谢了莱布尼兹和伯努利,尤其是对自己的恩师约翰·伯努利进行了感谢。
因此说,洛必达是一个值得尊敬的学者和传播者,他为这项事业贡献了自己的一生。
而对约翰·伯努利,他的一生也是天才展现的一生!
他生于声名显赫的伯努利家族,这个家族三代人诞生了8位大科学家、120多位研究学者等,在数学、科学、技术、工程乃至法律、管理、文学、艺术等方面都享有厚重的名望,有的甚至影响了全世界。
约翰·伯努利的数学成果丰硕,例如解决悬链线问题(1691年)、提出洛必达法则(1694年)、最速降线(1696年)和测地线问题(1697年),给出求积分的变量替换法(1699年),研究弦振动问题(1727年),出版《积分学教程》(1742年)等。
约翰·伯努利的另一大功绩是培养了一大批出色的数学家,其中包括18世纪最著名的数学家欧拉、瑞士数学家克莱姆、法国数学家洛必达,以及他自己的儿子丹尼尔和侄子尼古拉二世等。
人的一生啊,有幸生活在一个天才辈出、百家争鸣的时代,亦或是亲历者,亦或是参与者,甚至自己就是开创者,那么也是一件很美的事情呐!!!
祝你取得理想的高考成绩!
,




