王林,王海新
(西安理工大学 自动化与信息工程学院,陕西 西安 710048)
针对层次聚类算法存在复杂度高、准确度低等问题,提出了一种基于最大生成树的社团划分算法。该算法重新定义了节点间相似度,并利用最大生成树进行初始聚类,然后根据社团相似度合并局部社团得到最终划分结果。算法不仅降低了时间复杂度,而且在划分社团的准确度方面有所提高。将该方法在真实网络与人工网络上进行验证和比对,实验结果表明基于最大生成树的社团划分算法能够快速、准确地划分出网络中的社团结构。
:社团划分;层次聚类;最大生成树;节点相似度
:TN929.12文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.07.005
引用格式:王林,王海新.基于最大生成树的社团划分算法[J].微型机与应用,2017,36(7):15-18.
0引言
随着社会的发展与进步,现实世界涌现出越来越多的复杂系统,许多复杂系统都可以直接或间接地以复杂网络的形式存在。因此,复杂网络一直是各个学科领域的研究热点。而社团结构是复杂网络中的一个重要属性,复杂网络中同一社团内节点之间连接紧密、而不同社团内的节点之间连接稀疏[1 2]。社团结构对于分析和了解整个网络的结构、功能及特性具有重要的意义[3]。
层次聚类算法是一类重要的社团划分算法,它从节点出发利用节点间的相似度分层次地进行聚类,然后利用模块度函数来确定社团的最优划分。层次聚类算法主要分为两种:一种是分裂式的方法,具有代表性的算法是GN算法[4],它通过不断计算边介数并移除边介数最大的边来划分复杂网络的社团,但是由于计算边介数的代价较大,导致GN算法的复杂度比较高[5];另一种是凝聚式算法,如Newman快速算法[6],通过不断合并节点并计算合并后的模块度增量Q,选择Q增加最多或者减少最小的合并方式进行社团合并,该算法在计算时间上比GN算法有了很大改善。之后,Clauset等人提出了CNM算法[7],通过结合堆和二叉树,对Newman快速算法进行了改进,使算法不仅计算高效,而且节省存储空间;但是CNM算法在划分社团时准确度却不高[8]。Blondel等人提出了BGLL算法[9],该算法起始时将网络中每一个顶点视为一个局部社团,网络朝着模块度增量改变最大的方向进行合并,直到模块度增量小于零。该算法简单、快速,但划分的结果受到模块度分辨率的限制,算法准确度低[10]。Eustace等人[11]提出了一种基于局部社团合并的方法,通过重新定义节点与节点、节点与社团、社团与社团之间的相似度来衡量它们之间的关系,通过不断合并节点或社团来达到划分社团的目的,但是该算法容易陷入局部最优解。由上可知,已有的层次聚类算法普遍存在计算速度快但准确度低的问题。
针对上述研究中所出现的问题,本文提出了一种新的层次聚类算法,该算法在最大生成树上对社团进行初始聚类,然后逐步合并局部社团得到社团结构。而最大生成树包含网络中所有节点,但是不包括所有边,因此在最大生成树上进行社团划分可以降低算法复杂度[12]。此外,相比传统的相似度度量方式,本文定义了一种新的节点相似度公式,它不仅考虑到网络局部信息,而且兼顾网络的全局信息,使得算法的准确性得到进一步提高。
1最大生成树
一个连通且不存在回路的图称为树,如果一个图G的生成子图T是树,则称它为G的生成树,一个加权的最大生成树是G的具有最大权值的生成树。对于一个给定网络G(V,E),其中V是节点集合,E是边集合。在计算它的最大生成树之前先要为每条边赋值,本文使用节点相似度作为每条边的权值,记为ω(vk,vk 1),其中vk、vk 1分别为第k个节点和第k 1个节点,这里相似度等于两节点的共同邻居节点个数与所有的邻居节点个数之比。构建其最大生成树首先从一棵空树T开始,往集合T中逐条选择并加入权值最大的n-1条边,最终生成一棵包含n个节点和n-1条边的最大生成树。构建最大生成树的步骤如下:
(1)初始化集合Vnew={x}和Enew={},其中x为起始节点;
(2)在边集E中选择权值最大的边<u,v>加入集合Enew中,其中u为集合Vnew中的元素,节点v∈V但v不在集合Vnew当中。
(3)重复步骤(2),直到所有节点都被加入到集合Vnew中。
2利用最大生成树划分社团结构
本文算法聚类部分分为两个阶段:第一阶段是网络的初始聚类,就是在最大生成树上对节点进行聚类得到局部社团;第二阶段是迭代合并第一阶段产生的局部社团,直到所有的局部社团都被合并到一个社团,然后根据Q值选取网络社团结构的最佳划分。
2.1节点聚类
这一阶段主要是在最大生成树上把节点聚类成局部社团,即是将最大生成树上的节点与其最相似的核节点合并为一个局部社团。
节点聚类之前首先要找到生成树上所有的核节点。对于一个节点u,其与邻居节点的边权值大于ε的集合为:
Γε(u,v)={v∈Nghb(u)|ω(u,v) ε}(1)
其中ω(u,v)为边的权值。若|Γε(u,v)|>μ,则u是一个核节点。参数ε对核节点的确定有很大影响,本文使用最大生成树的边权值集合作为ε的候选集合。为使节点准确地划分到局部社团中,本文新定义了一个节点相似度公式,该公式将节点间路径考虑进去,这样就同时兼顾了局部信息和网络的全局拓扑结构,能够更加准确地衡量节点间的相似度。其相似度公式定义如下:
其中,ω(vk,vk 1)表示节点与其邻居节点之间的边权值,p(s,t)是节点s与t之间的路径。
2.2局部社团合并
第二阶段任务就是合并局部社团,但在合并之前首先判断是否存在核节点直接相连接的情况。若存在且它们的边权值大于参数ε,则可直接将这种核节点所在的局部社团进行合并;反之,则迭代合并社团相似度[13]最大的两个局部社团,这种迭代一直持续到整个网络呈现为仅有的一个大社团。其社团相似度公式定义如下:
式(3)中num(ci,cj)表示社团ci和cj相连的边的数量;式(4)中degree(vj)表示社团ci中任意一点的度值。
每次合并社团后都要计算相应的网络模块度,最终选择模块度最大时对应的社团结构作为最优划分。
2.3算法步骤及复杂度分析
本文算法步骤如下:
输入:一个无向无权网络G(V,E);
输出:网络的社团结构,Q值及参数ε的值;
(1)生成最大生成树:首先计算网络中每条边的权值,将无向无权网络G(V,E)转换成加权网络G(V,E,W),然后生成网络的最大生成树T(V,ET);
(2)确定核节点:对T(V,ET)上边的权值进行排序并记录到队列WT中,在候选队列WT中选择一个新值作为ε的值,然后在最大生成树T(V,ET)上根据式(1)计算出所有的核节点;
(3)节点聚类:计算所有节点到所有核节点的相似度S(s,t),并选择与其相似度最大的核节点进行合并,由此产生各个局部社团。判断核节点之间是否存在直接连边,且它们的相似度值S(s,t)>ε,如果存在就将这两个核节点所在的局部社团直接合并;
(4)局部社团合并:计算局部社团间的相似度,选择相似度最大的两个局部社团进行合并,然后计算并记录Q值;
(5)重复步骤(4)直到网络合并为一个社团,找到最大的Q值并记录到队列Qs中;
(6)判断队列WT中的值是否被完全遍历,如果没有则重复步骤(2)~(5),如果完全遍历则算法结束,选择Qs中最大的Q值及其对应的社团结构和ε进行输出。
假定网络中节点个数是n,边数是m,则计算最大生成树在最坏情况下的复杂度为O(mlogn);假定最大生成树上的核节点数目为k,计算节点与各个核节点相似度的复杂度为nk;k个核节点聚类成k个局部社团,将这k个局部社团聚类成一个社团需要k-1步,因此局部社团合并的时间复杂度为k-1;由于算法中将最大生成树T(V,ET)上的边权值作为ε的候选集合,因此在最坏的情况下,上述过程要重复执行n-1次。综上,基于最大生成树的社团划分算法在整个运行过程中的时间复杂度为O(mn)。
3实验结果及分析
通过本文算法对真实网络进行社团划分,然后利用人工网络对该算法的运行时间和准确性进行分析。实验在一台4核2.3 GHz的CPU、4 GB RAM 的笔记本电脑上运行,使用MATLAB软件进行编程和仿真,使用Gephi软件对实验结果进行处理和可视化。
3.1真实网络
在这里,选择Zachary空手道俱乐部网作为真实网络。利用本文算法首先计算出俱乐部网的最大生成树,然后在最大生成树上进行初始聚类,初始聚类结果如图1所示。
图1中交替使用灰和白两种节点颜色表示局部社团,同一颜色的节点被聚类到相同的局部社团中,这些社团再继续聚类而形成不同的社团结构。当μ=3,ε=0.334时,最大生成树上节点7、2、4、33、34都为核节点,由于核节点33、34直接相连且它们的权值为0.526大于ε,所以它们可以直接合并。本文提出的算法在俱乐部网上的最大Q值为0.373 3,在最大Q值时网络划分为两个社团,其结果如图2所示。

3.2计算机生成网
为了进一步衡量算法的准确度,将本文算法在LFR计算机生成网上与其他算法进行比较。网络的相应参数设置如下:网络节点数为N=1 000,平均度数Davg=4.8,最大度为Dmax=50,最小社团节点数Cmin=20,最大社团节点数Cmax=100。mu值为可变参数,它反映处于不同社团之间的边在所有边中所占的比例。mu值越大,表示处于不同社团之间的边越多,社团结构就越不明显[14]。
3.2.1准确性验证
社团划分的准确度用归一化互信息(Normalized mutual information)[15]来衡量,它的定义如下:
NMI值表示Y划分与X划分的接近程度,其中X表示网络的正确划分,Y表示算法得出的社团划分;它是一个介于0与1之间的数,NMI值越接近1表示算法划分出的社团结构准确度越高。
图3给出了本文算法与CNM算法和BGLL算法在不同mu值下对计算机生成网划分准确度的对比。
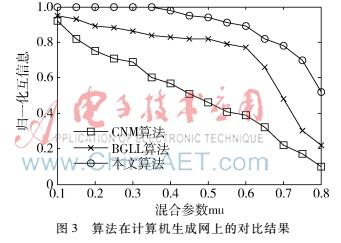
在混合参数mu<0.4时算法能完全正确地划分出社团,随着mu的增加,社团结构变得越来越模糊,算法的准确度也随之下降,但其NMI始终大于CNM算法和BGLL算法。图3表明,本文算法对计算机生成网的划分结果要优于CNM算法和BGLL算法。
3.2.2复杂度验证
为了评估本文算法的运行时间效率,选择快速Newman算法和CNM算法作为对比,其结果如图4所示。

其中节点数目分别从1 000增长到5 000,边数目为节点数目的10倍。方格线代表CNM算法,圆圈线代表Newman快速算法,十字线代表本文算法。从图中可以看出,本文算法的运行时间效率要优于快速Newman算法,而CNM算法的复杂度近似线性。本文算法虽然在运行速度上略逊于CNM算法,但是在算法准确度上比CNM算法高,且本文复杂度在可接受的范围内。
4结论与展望
针对现有的层次聚类算法复杂度高、准确度低等问题,本文提出了一种基于最大生成树的层次聚类算法。该算法首先在最大生成树上找到核节点,然后根据其他节点与核节点的相似度聚类成局部社团,最后逐步合并局部社团得到最优划分结果。算法在初次聚类时的相似度度量方法充分考虑了局部信息与全局信息,极大地提高了算法的准确度。实验结果证明,基于最大生成树的社团划分算法在执行效率和结果的可靠性方面优于已有的社团划分算法。在今后的工作中,通过对参数ε选取方式的改进,有可能进一步降低时间复杂度。
参考文献
[1] 王天成, 刘真真, 李天明,等. 复杂网络社团结构划分方法及其应用[J]. 信息通信, 2015(8):43-45.
[2] 郑浩原, 黄战. 复杂网络社区挖掘——改进的层次聚类算法[J]. 微型机与应用, 2011, 30(16):85-88.
[3] 赵晓慧, 刘微, 谢凤宏,等. 基于局部信息的复杂网络社团结构发现算法[J]. 微型机与应用, 2011, 30(15):43-46.
[4] GIRVAN M, NEWMAN M E J. Community structure in social and biological networks [J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12):7821-7826.
[5]李晓佳, 张鹏, 狄增如,等. 复杂网络中的社团结构[J]. 复杂系统与复杂性科学, 2008, 5(3):19-42.
[6] NEWMAN M E. Fast algorithm for detecting community structure in networks [J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2004, 69(6):066133.
[7] CLAUSET A, NEWMAN M E, MOORE C. Finding community structure in very large networks [J]. Physical Review E, 2005, 70(6 Pt 2):264-277.
[8] 吴蔚蔚, 刘功申, 黄晨. 基于相似度的社团划分算法[J]. 计算机工程, 2015, 41(11):67-72.
[9] BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks [J]. Journal of Statistical Mechanics Theory & Experiment, 2008, 2008(10):155-168.
[10] EUSTACE J, WANG X, CUI Y. Community detection using local neighborhood in complex networks [J]. Physica A Statistical Mechanics & Its Applications, 2015, 436:665-677.
[11] 李争光, 宋利. 基于结点相似性的层次化社团发现算法[J]. 信息技术, 2012(5):82-87.
[12] BEHERA R K, RATH S K, JENA M. Spanning tree based community detection using min-max modularity [J]. Procedia Computer Science, 2016, 93:1070-1076.
[13] SAOUD B, MOUSSAOUI A. Community detection in networks based on minimum spanning tree and modularity [J]. Physica A Statistical Mechanics & Its Applications, 2016, 460:230-234.
[14] 梁宗文, 杨帆, 李建平. 基于节点相似性度量的社团结构划分方法[J]. 计算机应用, 2015, 35(5):1213-1217.
[15] 王林, 高红艳, 王佰超. 基于局部相似性的K—means谱聚类算法[J]. 西安理工大学学报, 2013, 35(4):455-459.
,




