假设两个向量a=(x1,y1),b=(x2,y2),两个向量之间的夹角为θ,那么根据上篇文章中向量数量积的运算规则,可以很方便地用坐标值表示夹角的余弦值

在上述定义的基础上,我们假设向量a、b均为单位向量、向量起始点均在原点,那么两个向量的终点都落在单位圆上。

由任意角的三角函数在单位圆的定义可知,单位圆上的点对应角度的余弦值为其横坐标值、对应角度的正弦值为其纵坐标值。设向量a的终点对应角度为α,向量b的终点对应角度为β,那么对应的终点坐标为

易知,向量之间的夹角θ与两个角度的关系为

将上述等式带入等式(1)中并化简,可得

这个等式就是三角恒等变换中的两角差的余弦。
由这个等式进行简单变换便可得到其他三角恒等变换的表达式。
将等式(2)中的β替换成-β,可得

将等式(2)中的α替换成α-π/2,可得
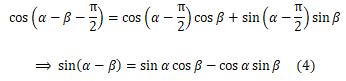
将等式(4)中的β替换成-β,可得

我们从向量的夹角公式,结合任意角在单位圆中的定义,经过简单变换,推导出了等式(2)(3)(4)(5)四个三角恒等变换公式。三角恒等变换公式不需要死记硬背,它们之间是可以利用诱导公式互相转化的,理解推导的思想更加重要。
本文由小朱与数学原创,欢迎关注,带你一起长知识!
,




