1、一个数列,设定最前面两个数是1、1,后面的每个数都是它前面的两个数之和。

即数列:1,1,2,3,5,8,13,21,34,55,89,144,233……这个数列称为"斐波那契数列",这些数称为"斐波那契数"。
如果用相邻两个斐波那契数相除,会发现所得的数值越来越接近一个常数,其近似值约为0.618,而反过来相除所得的数值趋近于1.618。
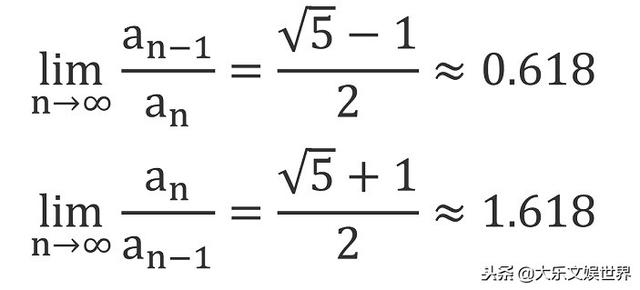
2、把某个整体分成两部分,如果使较大部分与整体部分的比值等于较小部分与较大部分的比值,这个比值为(√5-1):2,近似值为0.618。

3、将一个正五边形的所有对角线连接起来,所组成的所有三角形中,较短的边与较长的边的比值都是(√5-1):2,近似值为0.618。
…………
太多的巧合都指向了一个数值0.618,那么0.618这个数值到底是什么呢?这就是黄金分割。

黄金分割的数学定义:把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大部分的比值,这个比值即为黄金分割,通常用古希腊字母Ф表示。其比值是(√5-1):2,近似值为0.618。

黄金分割这个比值非常有趣,通过计算可以发现,黄金分割的平方等于1减去黄金分割,黄金分割的倒数等于1加上黄金分割,1与1加上黄金分割的比值还是黄金分割。

黄金分割首先是由毕达哥拉斯发现的,被认为是最理想的比例。其和谐性和艺术性,能够给人美感,有着广泛的应用。
画家在画画时,按黄金分割比例(即0.618∶1)来画腿长与身高,画出的人体身材最舒适优美。
建筑师在设计时,按黄金分割比例设计门窗、殿堂等,会更加协调,令人赏心悦目。
…………
,




