内容转载自 初级电路与软件研究
运算放大器(operational amplifier),简称:运放(op amp),是一种集成的放大器,它的特点是电压增益非常大(通常为几万以上),同时输入阻抗高、输出阻抗低,是一种比较理想的放大器。至于为什么要在它的名称前加上“运算”两字,是因为最初这个器件是用来做计算的用的。
现在我们一提到计算机,肯定是指数字计算机,但当年可不是这样。在上世纪40年代的时候,数字计算机的发展还刚刚起步,运算速度慢,价格昂贵,发展前景还不是很明朗。当年的很多计算工作都是靠模拟计算机来完成的,虽然模拟计算机的计算结果并不是很精确,但其结构简单,成本低廉,运算速度快,很多情况下还是可以一用的(稍后我们会介绍如何用运放来构成加减法电路、积分微分电路)。后来,人们渐渐发明了运放的很多其他用途,例如:微信号放大器、比较器、振荡器、有源滤波器等等。
1. 理想运算放大器
对于理想运放,我们对其做如下假设:开环电压增益为无穷大、输入阻抗为无穷大、输出阻抗为0。其模型符号如下图所示:

图8-01.01
对于vi1,其输入端带一个“ ”号,我们称其为:同相输入端(noninverting input)。对于vi2,其输入端带一个“-”号,我们称其为:'反向输入端'(inverting input)。
理想运放有以下两个重要特点:
- [1] 输入电流为0;
- [2] 两个输入端的电压差永远为0。
第[1]点输入电流为0很好理解,因为我们将运放的输入阻抗视为无穷大了,所以近似于开路。但是第[2]点就有些魔幻了,对于一般的电路,只有在两个端子之间连一根电线让它们短路,才能保证这两个端子的电压差永远为0。但由于第[1]点的限制,理想运放的两个输入端子中没有任何电流流过,因此不是短路;但这两个端子的电压差又时刻保持为0,就好像隔空同步一样,因此有一个专门的名称描述这一现象,称为:虚短(virtual short)。虽然在实际中没有这种魔幻的器件,但由于现在我们仅仅是抽象一个理想化模型,因此我可以接受这样的假设。后面的各种理想运放电路的分析,都是基于理想运放这两个特点展开的。(说句题外话,如果你再往后学习了信号处理与分析的相关知识,你就会理解,虚短是由于运放内部深度负反馈的设计造成的必然结果。)
我们再来看输出,既然两个输入端的电压差为0,电压放大倍数又为无穷大,那输出电压到底是多少,0乘以无穷大是多少?这个就是理想运放的又一个魔幻点,由于0乘以无穷大可以为任意值,因此理想运放的输出也可以为任意值,具体会输出多少伏电压,完全由外电路的配置决定。
(顺便先提一下,在实际的运放器件中,输入电流不完全为0,而是有及其微小的电流流入运放;且两个输入端子之间的电压差也不完全为0,而是有很小的几个微伏的电压。正是这个几微伏的电压,乘以几万量级的电压增益后,才能得到一个几伏~十几伏的输出电压,并且,能够输出的最大电压受到运放器件供电电压VCC的限制。)
2. 反相放大器
运放一个最基本的运用就是用来放大电压信号,虽说其开环电压增益为无穷大,但我们并不是要使输入信号放大无穷大倍。就像我们在前面介绍过的各种BJT与FET放大电路那样,我们要的是通过配置外围电路的电阻值,来得到我们想要的电压放大倍数。
一个最简单的的使用运放的放大电路如下图所示(这里输入输出电压都用交流相量符号表示):

图8-01.02
电路工作情况分析如下:
电路的同相工作端接地,电压值为0V,根据理想运放的虚短特点,V1点的电压也必须为0V,然后根据欧姆定律,流过电阻R1的电流为:

由于理想运放的输入端不能有任何电流流入,因此电流I1不会被分流,而全部流向Rf,根据欧姆定律,输出端的电压Vo为:

电路的实际电压增益为:

其中的负号表明,输出电压与输入电压极性相反,因此这个结构的放大电路称为:反相放大器(inverting amplifier),有时也称为:反相比例放大器。
由于输出到输入之间有一个电阻Rf的存在,其作用是建立了输出到输入之间的一个反馈通道,不像开环增益那样是纯单向的增益,因此这个电路的实际电压增益也称为:闭环增益。闭环增益一般会比开环增益小得多,且其值不是取决于器件的原始性能,而是取决于电路的结构和配置。
3. 同相放大器
同相放大器的电路结构如下图所示:
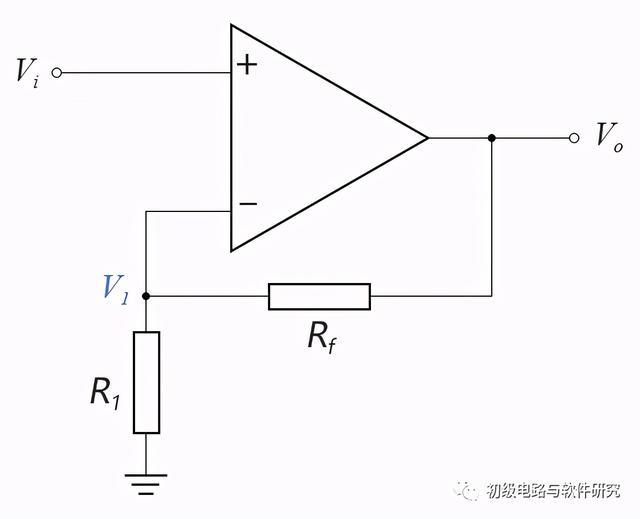
图8-01.03
电路工作情况分析如下:
运放的反相输入端电压V1根据欧姆定律,计算式为:

根据理想运放的虚短特点,V1点的电压与输入电压Vi相等,故上式可写为:

因此电路的的实际电压增益为:

电压增益的表达式中没有负号,输出电压与输入电压极性相同,因此这个结构的放大电路称为:同相放大器(noninvertingamplifier)。
,




