七年级有理数单元考
一.选择题(共6小题)
1.四个数﹣3,0,1,π中的负数是( )
A.﹣3B.0C.1D.π
【解答】解:四个数﹣3,0,1,π中的负数是﹣3.
故选:A.
2.对于﹣a表示的数理解不正确的是( )
A.一定是负数B.可以表示a的相反数
C.有可能是正数D.有可能是0
【解答】解:A、当a=0时,﹣a=0,0既不是正数,也不是负数,故本选项正确;
B、﹣a可以表示a的相反数,故本选项错误;
C、当a<0时,﹣a>0,即﹣a有可能是正数,故本选项错误;
D、当a=0时,﹣a=0,即﹣a表示0,故本选项错误;
故选:A.
3.下列式子中成立的是( )
A.﹣|﹣5|>4B.﹣3<|﹣3|C.﹣|﹣4|=4D.|﹣5.5|<5
【解答】解:A.﹣|﹣5|=﹣5<4,故A选项错误;
B.|﹣3|=3>﹣3,故B选项正确;
C.﹣|﹣4|=﹣4≠4,故C选项错误;
D.|﹣5.5|=5.5>5,故D选项错误;
故选:B.
4.下列说法正确的是( )
A.0.750精确到百分位B.3.079×104精确到千分位
C.38万精确到个位D.2.80×105精确到千位
【解答】解:A、0.750精确到千分位,故本选项错误;
B、3.079×104精确到十位,故本选项错误;
C、38万精确到万位,故本选项错误;
D、2.80×105精确到千位,故本选项正确;
故选:D.
5.在数轴上,与表示数﹣1的点的距离是2的点表示的数是( )
A.1B.3C.±2D.1或﹣3
【解答】解:在数轴上,与表示数﹣1的点的距离是2的点表示的数有两个:﹣1﹣2=﹣3;﹣1 2=1.
故选:D.
6.给定一列按规律排列的数:

,则这列数的第6个数是( )
A.

B.
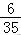
C.

D.

【解答】解:∵一列按规律排列的数:

∴这列数的第5个数是:

=

,
这列数的第6个数是:

=

,
故选:A.
二.填空题(共4小题)
的相反数是

.
【解答】解:
的相反数为

,
故答案为:

(-1)2018 (-1)2017= 0
【解答】解:1-1=0
故答案为:0
9.若
,则1-a= -5或7
【解答】解:a=
,
所以a=6时,1-a=1-6=-5
a=-6时,1-a=1-(-6)=7
故答案为:-5、7
10.若a、b互为相反数,c、d互为倒数,|x|=3,则式子2(a b)﹣(﹣cd)2017 x的值为 4或﹣2 .
【解答】解:根据题意得:a b=0,cd=1,x=3或﹣3,
当x=3时,原式=0 1 3=4;当x=﹣3时,原式=0 1﹣3=﹣2,
故答案为:4或﹣2
11.太阳的半径约是696000千米,用科学记数法表示(精确到万位)约是 7.0×105 千米.
【解答】解:696000=6.96×105≈7.0×105,
故答案为:7.0×105.
12.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a b c= 110 .

【解答】解:根据左上角 4=左下角,左上角 3=右上角,右下角的数为左下和右上的积加上1的和,
可得6 4=a,6 3=c,ac 1=b,
可得:a=10,c=9,b=91,
所以a b c=10 9 91=110,
故答案为:110
解答题(共5小题)
5×(-2) (-8)÷(-2)
= -6
[2-5×(-
)2]÷(-)
= 1
15.(-24)×(
)
= -37
16.-14-(1-0×4)÷
×[(-2)2-6]
=5
17.小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是3km/h,那么小明跑步一共用了多长时间?

【解答】解:(1)如图所示:
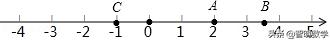
(2)小彬家与学校的距离是:2﹣(﹣1)=3(km).
故小彬家与学校之间的距离是3km;
(3)小明一共跑了(2 1.5 1)×2=9(km),
小明跑步一共用的时间是:9÷3=3(小时).
答:小明跑步一共用了3小时.
18.某人用400元购买了8套儿童服装,准备以一定的价格出售,如果每套儿童服装以55元的价格为标准,超出的记作正数,不足的记作负数,记录如下(单位:元): 2,﹣3, 2, 1,﹣2,﹣1,0,﹣2,当他卖完这8套儿童服装后是盈利还是亏损?盈利(或亏损)多少?
【解答】解:根据题意得
2﹣3 2 1﹣2﹣1 0﹣2=﹣3,
55×8 (﹣3)=437元,
∵437>400,
∴卖完后是盈利;
437﹣400=37元,
故盈利37元.
19.(1)通过观察、计算,探索规律:
32﹣12=4×2=(3 1)(3﹣1)
52﹣22=7×3=(5 2)(5﹣2)
82﹣32=11×5=(8 3)(8﹣3)
72﹣42= 11×3=(7 4)(7﹣4) ;
请用你发现的规律填空:a2﹣b2= (a b)(a﹣b) ;
(2)观察下面由※组成的图案和算式,解答问题:
1 3=4=22
1 3 5=9=32
1 3 5 7=16=42
1 3 5 7 9=25=52
①请猜想1 3 5 7 9 … 19= 102 ;
②请猜想1 3 5 7 9 … (2n﹣1) (2n 1) (2n 3)= (n 2)2 .

【解答】解:(1)72﹣42=11×3=(7 4)(7﹣4);
a2﹣b2=(a b)(a﹣b);
(2)①1 3 5 7 9 … 19=102;
②1 3 5 7 9 … (2n﹣1) (2n 1) (2n 3)=(n 2)2.
故答案为11×3=(7 4)(7﹣4);(a b)(a﹣b);102;(n 2)2.
20.对于有理数a,b,定义一种新运算"⊙",规定a⊙b=|a b| |a﹣b|.
(1)计算3⊙(﹣4)的值;
(2)当a,b在数轴上的位置如图所示时,化简a⊙b.

【解答】解:(1)根据题意知:
3⊙(﹣4)=|3 (﹣4)| |3﹣(﹣4)|.
=1 8
=9;
(2)由图可知a<0<b,且|a|>|b|,
则a b<0、a﹣b<0,
∴a⊙b=|a b| |a﹣b|=﹣a﹣b﹣a b=﹣2a.
21.如图,数轴上有A,O,B三点,点O是数轴的原点,点B表示的数是10,AB=18.
(1)求点A表示的数;
(2)红、蓝、黑三只蚂蚁分别从点A,O,B三点同时出发沿数轴向右爬行,红蚂蚁的速度是每秒12个单位长度,蓝蚂蚁的速度是每秒10个长度单位,黑蚂蚁的速度是每秒8个长度单位.
①若红蚂蚁与蓝蚂蚁在C点相遇,求C点所表示的数;
②他们出发几秒后,红蚂蚁与蓝蚂蚁、黑蚂蚁的距离相等?

【解答】解:(1)∵点B表示的数是10,AB=18,
∴A点表示﹣8;
(2)①设经过t秒红蚂蚁与蓝蚂蚁在C点相遇,
∵红蚂蚁的速度是每秒12个单位长度,蓝蚂蚁的速度是每秒10个长度单位,
∴

,
解得c=40.
答:C点所表示的数是40;
②当蓝蚂蚁被红蚂蚁超过在左侧,红蚂蚁在中间,黑蚂蚁在右侧时,
﹣8 12t﹣10t=10 8t﹣(12t﹣8),
解得t=

;
当蓝蚂蚁超过黑蚂蚁在右侧,红蚂蚁在中间,黑蚂蚁在左侧侧时,
﹣8 12t﹣(10 8t)=10t﹣(﹣8 12t),
解得t=

.
当蓝蚂蚁与黑蚂蚁相遇时,红蚂蚁到这两点的距离也相等.此时时间t=10÷(10﹣8)=5.
综上,t=

秒或t=5秒时红蚂蚁与蓝蚂蚁、黑蚂蚁的距离相等.
第1页(共1页)
,




