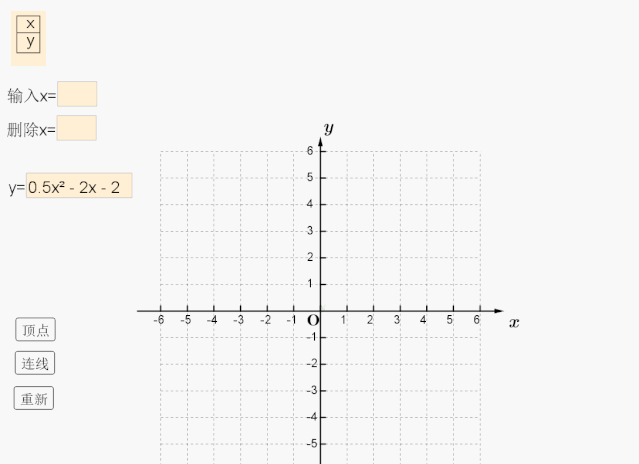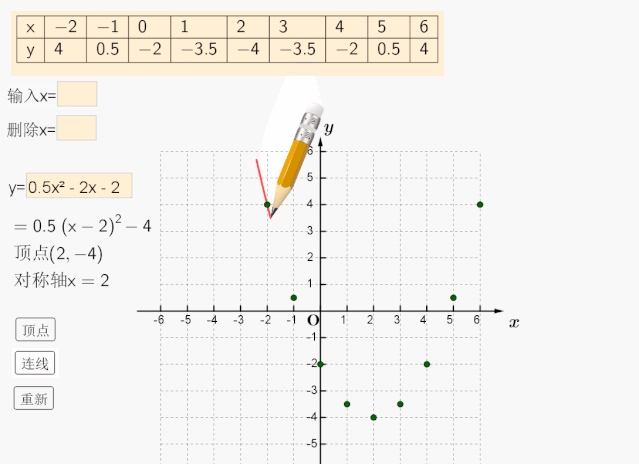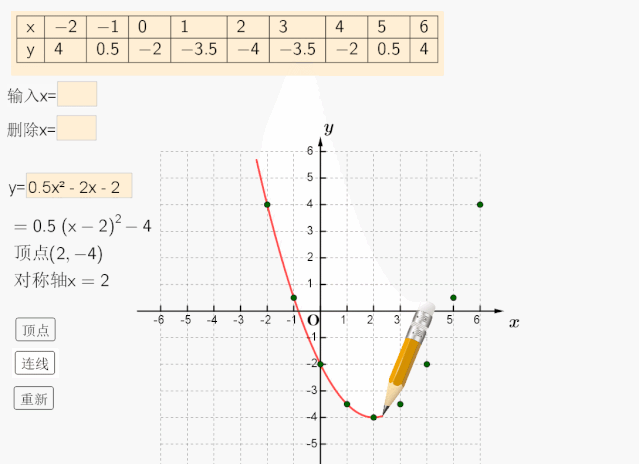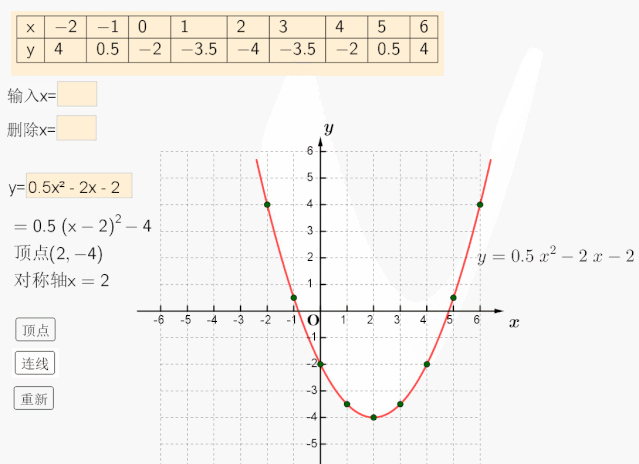y等于根号x的图像过原点和点(1,1),是一条抛物线的左半支绕原点旋转90度得到的图像。我们有三种方法可以画出这个图像。

第一种方法是最基础的,运用描点法来作y=根号x的图像。可以在平面直角坐标系中,分别取x=0, 1, 4, 9, 16,…,对应的y=0, 1, 2, 3, 4,…. ,然后用平滑的曲线把这些点连起来,就可以得到y=根号x的图像了。

可以看到y=根号x的图像只经过原点和第一象限,像开口向上的二次函数左支绕顶点(原点)旋转90度。这里其实是有内在联系的,因为y=根号x就是y=x^2(x>=0)的反函数。这就得到了画y=根号x的图像的第二种方法。
根据互为反函数的图像关于y=x对称,我们可以先作出y=x^2(x>=0)的图像,然后再作它关于y=x的轴对称图形,最后得到的这个图形就是y=根号x的图像。
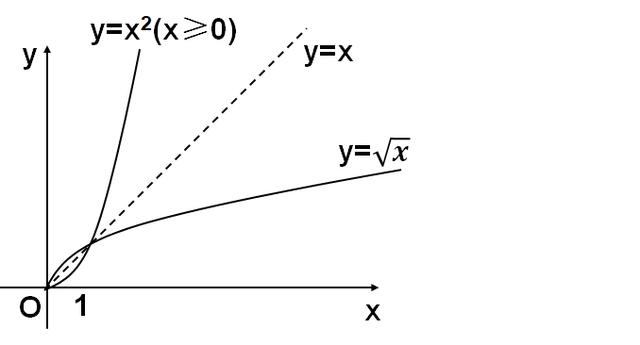
最后一种方法,是作函数图像比较通用的方法,就是根据函数的性质,来作它的图像。首先我们分析函数y=根号x的单调性,奇偶性,凹凸性和周期性。可以发现它是没有奇偶性和周期性的。
又由y=根号x的导函数y’=1/(2倍根号x)>0,可以知道它是一个严格单调递增函数。又y=根号x的二阶导函数y"=-1/(4倍根号(x^3))<0,可以知道,它是一个凸函数。这就对函数y=根号x的图像形状有了一个大概的了解。
接下来我们找函数图像与x轴和y轴的交点,当x=0时,y=0,发现函数图像经过原点。一个点还不够,我们再找另外一个点,当x=1时,y=1. 即函数的图像过点(1,1)。然后再求函数的渐近线。不难求得函数图像没有垂直渐近线。
又当x趋于正无穷大时,lim((根号x)/x)=0,可见函数最多有一条水平渐近线。又当x趋于正无穷大时lim根号x=正无穷大。可见函数连水平的渐近线都不存在。只能知道在x趋于正无穷大时,函数也趋于正无穷大。
既然这样,我们唯有求函数在x=0和x=1的切线方程,来确定函数图像的性状。当x=0时,y’=0,可见函数图像在x=0的切线是y轴。当x=1时, y'=1/2, 又b=1-1/2=1/2. 所以函数在x=1的切线方程是y=x 1/2. 这样我们就可以根据上面的信息,得到函数y=根号x的图像如下图:
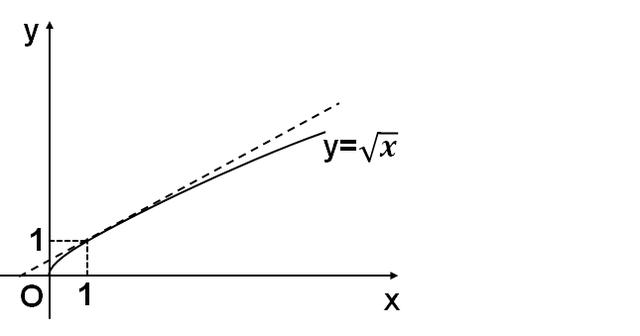
这三种画y=根号x的图像的方法,你更喜欢哪一种呢?
,