
特征:分数、百分数、比例、倍数
结论:如果 a:b = m:n,m、n为整数,m/n最简;
则 a是m的倍数, b是n的倍数,
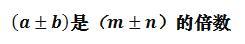
比例形式(a-b):a :b :(a b)= (m-n) : m : n : (m n)
例1:铺设一条自来水管道,甲队单独铺设 8 天可以完成,而乙队每天可铺设 50 米.如果甲、乙两队同时铺设,4 天可以完成全长的 2/3,这条管道全长是多少米?( ).
A.1000 B.1100 C.1200 D.1300
【解析】C
题干中有个明显的2/3分数,问的是管道全长,4天完成了管道全长的2/3,则管道全长必然是3的倍数,答案中有C符合。
抓住特征2/3,得到特征数3,直接秒杀,完全不需要列方程。
例2:甲、乙两种商品原来的单价和为 100 元,因市场变化,甲商品降价 10%,乙商品提价 40%,调价后两种商品的单价和比原来的单价和提高 20%,则乙商品提价后为多少元?
A. 40 B. 60 C. 36 D. 84
【解析】D
题干中有特征:10%、40%、20%,问的是乙商品提价后的价格,直接相关的特征数为40%=2/5,所以可以理解成乙商品原价是5份,提高了2份,提价后必然是7份,也就是7的倍数,答案只有D符合
例3:教室里有若干学生,走了10名女生后,男生是女生人数的2倍,又走了9名男生后,女生是男生人数的5倍。问最初教室有多少人?( )
A.15 B.20 C.25 D.30
【解析】C
题干中有特征:2倍、5倍,走了10名女生后男生是剩余女生的2倍,也就是总人数-10必然是3的倍数,只有C项符合(25-10=15,是3的倍数)
例4:甲、乙两车分别从 P、Q 两地同时出发,相向而行。相遇时,甲车比乙车多行驶 36 千米,乙车所行驶路程为甲车所行驶路程的 4/7,则P、Q两地相距( )千米
A.72 B.96 C.112 D.132
【解析】
题干中有个明显的4/7分数,快速反应4个特征数(3、4、7、11);问的是两地距离,两人一开始从两端出发中间相遇,求得是路程和,那路程和必然是11的倍数,只有D符合。
注意:看到分数4/7,很容易想到4和7,但是也不要忘了3和11。
总结:倍数特性在考场上经常用,虽然直接秒杀的到答案的题目不一定多,但是排除两个选项的经常有,也能大大提高准确率了,所以大家务必要掌握好倍数特性法。
来源:东亮教育(www.dlexam.net),供考生学习参考。
,




