
浮点数通常被写成如下的形式: X = Mx* 2Ex
浮点数通常有两种表示方式,一种表示方式用于运算过程,出现在浮点运算器内部,此时的Mx是浮点数的尾数,机器中多用原码表示,不使用隐藏位技术,是绝对值小于1的规格化的二进制小数。Ex为该浮点数的阶码, 机器中多用移码表示,一般为二进制整数,给出的是浮点数表示中的实际指数的幂 128(8位阶码时〕,而该指数的底通常选用2。另外一种表示用于浮点数的存储过程,对于规格化的非0值的浮点数使用隐藏位技术,即隐去规格化尾数最高一位上的数值1,剩余尾数再左移一位,并相应地把阶码部分的值减1,变为实际指数的幂 127(8位阶码)。这样做既不影响实际运算,保存过程中尾数又多一个bit的精度。
1.浮点加减法的运算步骤 假定有两个浮点数 X = Mx* 2Ex, Y = My * 2Ey 实现X±Y运算,要用如下多步完成: (1) 计算阶差操作,即比较两个浮点数的阶码值的大小,求△E=Ex-Ey。 (2)当阶差△E不等于零时,首先应使两个数取相同的阶码值。其实现方法是,把原来阶码小的数的尾数右移|△E|位,其阶码值取大的阶码值,则该浮点数的值不变(但精度变差了)。为减少误差,可用另外的线路,保留右移过程中移出去几位值,用于以后舍入。 (3) 实现尾数的加(减)运算,即对两个完成对阶后的浮点数执行求和(差)操作。 (4) 规格化处理,完成对不满足规格化规则的计算结果的规格化操作。 (5) 有时还需要执行舍入操作。舍入的总的原则是要有舍有入,而且尽量使舍和入的机会均等,以防止误差积累。常用的办法有”0”舍”1”入法,即移掉的最高位为1时则在尾数末位加1;移掉的最高位为0时则舍去移掉的数值。该方案的最大误差为2-(n 1)。另一种方法是恒“置1”法,即右移时,丢掉移出的那些低位上的值,并把结果的最低位置成1。还有更精确的舍入处理方案,在此不予介绍。 (6) 接下来还要判断结果的正确性,即检查溢出。浮点数的溢出是以其阶码溢出表现出来的。在加减运算真正结束前,要检查是否产生了溢出,若阶码正常,加(减)运算正常结束;若阶码下溢,要置运算结果为浮点形式的机器零,若上溢,则置溢出标志。
以Intel 80287浮点协处理器为例,来介绍浮点处理器的组成和运行方式。80287是Intel公司生产的、为配合Intel 80286或80386微处理器处理浮点数等而设计的选购件,在当前流行的微处理机系统中,性能更高的浮点运算器已集成到CPU芯片内。80287内部结构的逻辑框图如图所示。
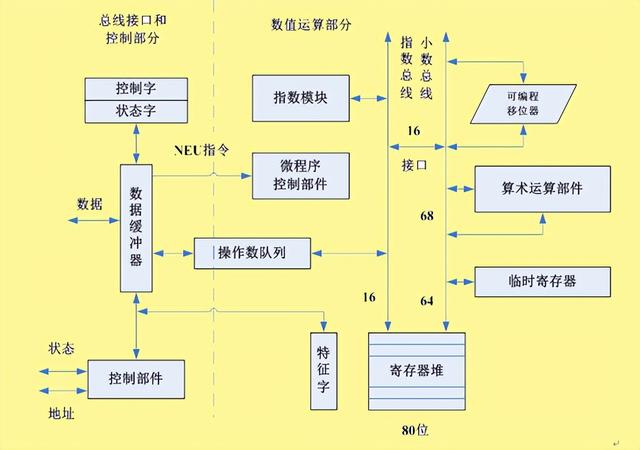
图 80287内部结构的逻辑框图
80287是被做在单个芯片之内,并用40条引线的外壳封装。它不是一个简单的浮点运算器本身,而且包括执行数据运算所需要的全部控制线路。 从图3.10可以看到,80287内部有处理浮点数指数部分的部件和处理尾数部分的部件,有加速移位操作的移位器线路,它们通过指数总线和小数总线与八个80位字长的寄存器堆栈相连接。这些寄存器可以按堆栈方式工作,此时,栈顶被用作累加器;也可以按寄存器的编号直接访问任意一个寄存器。 八个寄存器的编号用0到7表示,处在栈顶的那个寄存器的编号由80287的状态字字段TOP给出。在80287的指令中,用ST表示栈顶寄存器,并且可以用ST(i)来访问其它7个寄存器,此时i值可以为1-7中的一个值。i是相对于栈顶的一个偏移量,而不一定是真正八个寄存器的实际编号。 三种浮点数,阶码的基数均为2,阶码用移码表示,尾数用原码表示。浮点数有32位、64位和80位三种长度。80287在从存储器取数和向存储器写数时,均用80位的临时实数和其它数据类型执行自动转换。 为了保证指令的正确执行,80287内还设置了各为16位字长的三个寄存器,即特征字寄存器,控制字寄存器和状态字寄存器。 80287浮点协处理器的主要性能是: ♦可与80286或80386异步并行工作; ♦高性能的80位字长的内部结构,有8个80位字长的以堆栈方式管理的寄存器组; ♦浮点数的格式,完全符合IEEE制定的国际标准; ♦能处理包括二进制浮点数、二进制整数和十进制数串三大类共7种数据; ♦扩展了80286或80386的硬件指令,直接支持对7种数据的指数、对数、三角函数和其它一些数学函数的计算; ♦内部的出错管理功能。
,




