大部分人都知道线性代数是学习任何技术学科都需要掌握的科目之一。而且我也注意到初次学习线性代数的学生往往对这一科目的理解很肤浅。

学生在教室中学到的可能是如何进行各种各样的计算。比如矩阵乘法、行列式的计算。但是结果很可能是学生并非真正理解为什么矩阵乘法要如此定义。也并不知叉积与行列式有所关联,或者特征值究竟代表了什么?大部分时候学生对于矩阵的数值操作驾轻就熟。但是对于潜在的几何直观知之甚少。
在数值水平和几何水平上理解线性代数上有着根本性的差异。它们各有千秋,但是粗略的讲,几何水平上的理解能让你判断出解决特定问题需要用什么样的工具。感受到他们为什么有用以及如何解读最终结果。数值水平上的理解则能让你顺利利用这些工具。

假如你在学习线性代数时,并没有几何上的直观理解作为坚实基础。问题可能暂时不会浮出水面。但是当你在你的研究领域中继续钻研时,他就会显露出来。不管是计算机科学,工程学,统计学,经济学还是数学本身,这个道理都是一样的。当你坐在教室里或者你开始从事一项工作,都需要你通晓线性代数知识。你的教授或者同事所做的就如同魔法一般,他们很快就知道应该使用什么方法,以及答案大致是什么样子。如果你猜测他们处理的是繁杂无章的数据,你可能还会以为他们有什么奇特的计算方法。

打个比方,假如你首次学习正弦函数时,学到的是这样一个无穷次多项式。你的作业只是通过代入不同的数字,并做合理的截断,来练习计算正弦函数的近似值。再假设你对三角形和正弦函数的关系有一点模糊的认识。但是确切是什么关系你并不清楚,这也不是课程的重点所在。后来你参加了一门物理课程,正弦和余弦函数随处可见。其他人很快就知道如何使用这些函数。并且大致知道它的值是多少。你会觉得这很吓人对吧?仿佛那些适合做物理的人都有着计算机一般的大脑。而你在每个问题上都需要花费很长时间,蠢到无药可救。

线性代数也差不多如此,幸运的是和三角函数很类似。线性代数也有许多隐藏其中的直观理解,而且是可视化的直观理解。但是和三角函数的例子不同。线性代数中计算和可视化直观理解之间的联系往往相当直接。当你消化了这些内容,真正理解了几何直观和数值计算的关系。这门科目的细节和他在实际生活中的应用就会显得合情合理。
平心而论,目前很多教授也在努力向学生传达几何直观思想。但是我的确认为大部分课程让学生花在数值计算方面的时间太长了。尤其是在当今时代,我们有计算机来处理这些计算问题。在实践中人们关注的则是概念层面的东西。对于这个问题你能做的是形成正确的几何直观。以便在接下来的学习中收获累累硕果。同时对那些教授需要熟练掌握线性代数知识的课程的教育者来说。给学生一个途径指导他们快速重温线性代数知识。
由于大家有着不同的知识背景和接受程度,很难同时照顾到所有人。所以我鼓励大家必要时仔细思考。
线性代数中最基础最根源的组成部成部就是向量。所以我的确信我们在“向量究竟是什么”这一问题上达成共识。
一般来说有三种看待向量的观点,看似不同却有关联。分别将他们称为物理专业学生的视角,计算机专业学生的视角以及数学家的视角。从物理专业学生的视角看,向量是空间中的箭头,决定一个向量的是它的长度和它所指的方向,但是只要以上两个特征相同,你可以自由移动一个向量而保持它不变,

处在平面中的向量是二维的。而处在我们所生活的空间中的向量是三维的。

从计算机专业学生的视角看,向量是有序的数字列表。比如说你正在做一些有关房价的分析。而你只关心两个特征,房屋面积和价格。你可能会用一对数字对每个房屋进行建模。第一个数代表房屋面积,第二个数代表房屋价格。注意这里的数字顺序不可颠倒。用行话来讲,你会用二维向量对房屋进行建模。在这里“向量”只不过是“列表”的一个花哨的说法。之所以这个向量是二维的,是因为这个列表的长度是2。

另一方面,数学家试图去概括两种观点。大致的说,向量可以使任何东西。只要保证两个向量相加以及数字与向量相乘是有意义的即可。这种看待向量的观点相当抽象。这观点暗示了一个事实。即向量加法和向量数乘贯穿线性代数的始终,二者起着很重要的作用。
在谈论这些运算之前呢,我们先来确定一种思考向量的特定方式。每当引入一个关于向量的新主题时,我们需要你首先考虑一个箭头。更具体地说考虑这个箭头落在某个坐标系中比如x y平面。并且箭头起点位于原点。这与物理专业学生的看法略有不同。因为在他们眼中,向量可以在空间中自由落脚。但是在线性代数中向量经常以原点作为起点。
一旦你理解了“向量是空间中的箭头”这种观点。我们就来看看“向量是有序的数字列表”这种观点。我们可以通过向量坐标来理解他。我们中大部分都已经很熟悉坐标系这个概念的,我也很清楚这一点。但是这也值得再详细叙述一遍。因为这两种观点之间的碰撞恰恰形成了线性代数中重要的概念。
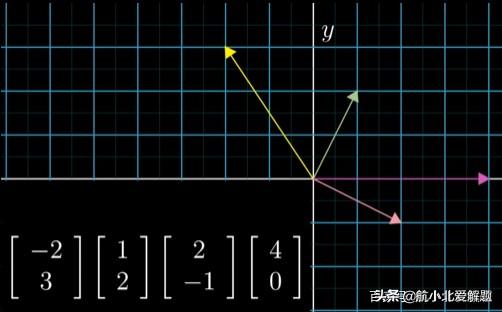
我们现在把眼光局限在二维空间中。画一条水平的线,我们叫他x轴。再画一条竖着的线,我们叫他y轴。两个轴的交点我们称之为原点。应该把它看作整个空间的中心和所有向量的根源。选取一个任意的长度代表1,你就可以在坐标轴上标记刻度来代表这一距离。一个向量的坐标由一对数构成。这种数教导你如何从原点也就是向量的起点出发到达它的尖端也就是向量的终点。第一个数告诉你,沿x轴走多远。正数代表向右移动,负数代表向左移动。第二个数告诉你在此之后沿着平行y轴的方向走多远。正数代表向上移动,负数代表向下移动。
为了把向量和点区别开,惯用的方法把这对数竖着写,然后用方括号括起来。每一对数给出唯一一个向量。而每一个向量恰好对应唯一一对数。

三维空间的向量又如何呢?那我们就在添加垂直于x和y轴的第三根轴叫他z轴。这种情况下每个向量就与一个有序的三元数组对应。每一个三元数组给出唯一一个向量。而每一个向量恰好对于唯一一个三元数组。现在我们回到向量加法和向量数乘。毕竟线性代数中每一个主题都围绕这两种运算。两种运算的定义都很直接。假设这里有两个向量,一个指向上方略微偏右。另一个指向右方略微偏下。为了把它们相加,我们平移第二个向量,使它的起点与第一个向量的终点重合。然后画一个向量,它从第一个向量的起点出发指向第二个向量的终点。这个向量就是他们的和。
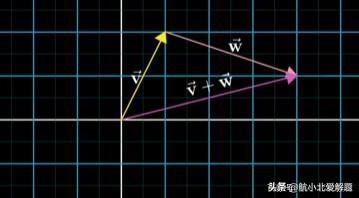
我们习惯上把向量看作是一种特定的运动,即在空间中朝着一个方向迈出一定距离。现在我们从数字的角度看看向量的加法。第一个向量的坐标是〔1,2〕,第二个向量的坐标是〔3,-1〕。那么新向量的坐标就是〔1 2,2 (-1)〕总得来说,在“向量是有序的数字列表”观点里。向量加法就是把对应项相加。

另一个基础的向量运算就是向量数乘。先看几个例子来更好地理解这个概念。比如说你选择数字2,把它与一个给定向量相乘。意味着你把这个向量拉长为原向量的两倍。再比如,如果将向量乘以1/3,就意味着这个线的长度缩短为原来的1/3。如果与一个负数相乘,那么首先这个向量反向,然后延长为原来的多少倍。这种拉伸或者压缩有时又使向量反向的过程被称为缩放。
实际上自始至终数字在线性代数中起到的主要作用就是缩放向量。所以通常“标量”和“数字”两个词在这里可以相互替换。
另一方面从数字的角度来看将一个向量伸长为原来的两倍,对于将每一个分量分别乘以2,所以将向量看作一个数字列表时,向量与标量相乘,就是将向量中的每个分量与标量相乘。实际上无论你怎么看待向量都无所谓。或把向量看作空间中的箭头。这种观点恰好有漂亮的数字表示与之对应。或者把向量看着数字列表,这种观点又恰好有漂亮的几何意义与之对应。
线性代数的效用很少体现在这些观点中的其中一个,更多体现在它能够在这些观点中相互转化。

线性代数为数据分析提供了一条将大量数据列表概念化、可视化的渠道。他让数字样式变得非常明晰。并让你大致了解特定运算的意义。另一方面,线性代数给物理学家和计算机图形程序员提供了一种语言。让他们通过计算机能处理的数字来描述并操纵空间。






