本文为“第三届数学文化征文比赛
《走近杨辉 揭秘三角》课堂实录
作者: 何萍
作品编号:057
一、温故知新
师:同学们,我们一起回忆前面学习过的多项式与多项式相乘运算法则。
生(全体):多项式与多项式相乘:多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。(PPT显示)
师:同学们刚才回答了多项式与多项式相乘运算法则的文字语言描述,我们初中阶段注重文字语言、图形语言以及符号语言三种语言的表述,所以它对应的符号语言是什么呢?
生(全体):(a b)(m n)=am an bm bn(PPT显示)
师:学习多项式与多项式相乘运算法则之后,我们学习了哪些特殊的公式呢?
生1:完全平方公式
生2:平方差公式。
师:这两类公式非常重要,同学们能否用符号语言表述完全平方公式呢?
生(全体):。
【设计意图】复习多项式乘以多项式运算法则的基础上,引导学生计算(a b)的高次幂,为提取展开式系数做好铺垫。
二、新知探究
活动一:
师:上课前请同学们完成了预习学案,接下来我们一起校对。
(投影学生作品)投影学案内容:
1.利用整式的乘法公式计算(结果依照a的次数从大到小的顺序排列)
师:第一道题要求同学们按照a的降幂排列,写出、、、(a b≠0)的展开式。
学生完成习题结果:

投影学案内容:
2.按行写出上题中各项展开式系数。
第1行:1
第2行:1 1
第3行:1 2 1
第4行:1 3 3 1
第5行:1 4 6 4 1
第6行:1 5 10 10 5 1
第7行:1 6 15 20 15 6 1
师:同学们完成得很棒!我们把完成的展开式系数填入下表中。
PPT显示:

师:我们给这些展开式系数拍合影,大合照变换队形。
PPT显示:

师:像这样的数字形成的图形像什么图形呢?
生(全体):三角形、等腰三角形。
师:非常好,这些数字组成的图形是三角形,我们称这个三角形系数表为杨辉三角。
【设计意图】通过学生自主演算,实践操作得出展开式系数,将展开式系数变换队形后,正好形成三角形系数表,从“形”的角度,揭示杨辉三角的第一层面纱。
活动二:
师:同学们,能否继续写出、、、...、的展开式系数?
生1:可以!我们可以继续利用多项式与多项式相乘运算法则运算。
师:同学们,以往解决含n的题型,如何解决?
生2:根据题目已有较简单的情况,逐步推导,写出规律,总结归纳规律,写出第n种情况。
师:说的真好!所以我们求的展开式系数是不是可以用类比的方法,根据已有的、、、、、、(a b≠0)的展开式系数,即已有的杨辉三角数据探究规律,从而根据规律得出的展开式系数。
师:接下来请同学们观察杨辉三角,寻找规律。
(给学生留有充足时间思考、讨论、交流、归纳)
生3:杨辉三角两条边都是1。
生4:每个数字都等于头顶上两个数字之和。
师:非常好,同学们观察出杨辉三角最重要、最基础的规律。
板演:规律1.两肩和。
师:同学们,还有什么规律呢?这个形状像什么呢?
生5:三角形!
生6:等腰三角形!
师:很好。这些数字组成的图形可以看作等腰三角形,等腰三角形的本质是什么图形呢?
生7:等腰三角形是轴对称图形。
师:真棒!等腰三角形是最典型的轴对称图形,:对称轴呢?
生8:中间一列数字。
师:我们可以发现画出对称轴,奇数行中间是数字,偶数行中间是空白,与首末两端“等距离”的两个数相等。所以,我们现在从“形”的角度发现杨辉三角第2个规律。
板演:规律2.对称性。
师:上面活动中,我们从“数形”两个角度看杨辉三角数与数之间的关系,那么把一部分数整体看待呢?比如把杨辉三角各行的数加起来的和,有什么特征吗?(给学生留有充足时间演算)
生9:经过计算,发现每行的和与2的高次方有关。比如第二行和为2,第三行和为4,第三行和为8,第四行和为16,第五行和为32,第六行和为64,这些数字正好都是2的次幂。
师:同学回答得非常棒,老师和同学们一起写出来。
(板演在黑板上)
板演:规律3.。
PPT显示:
规律之美1:杨辉三角中两条斜边都是由数字1组成,每一个数均为肩上两数之和。
PPT显示:
规律之美2:与首末两端“等距离”的两个数相等,杨辉三角具有对称性。
PPT显示:
规律之美3:杨辉三角第n行中n个数之和等于2的n-1次幂。
【设计意图】突出以学生为主体的课堂模式,引导学生自主观察杨辉三角形数表,直观感受数字的规律,学生通过探究从而归纳小结数字之间的关系。从“数”“形”两个角度分析杨辉三角数表后,引导学生从整体的眼光看待杨辉三角数表,即“横向”计算杨辉三角数表的和,寻找规律。同时,为后续从“斜向”观察杨辉三角的规律埋下伏笔。
师:通过以上活动,我们横着看、竖着看寻找规律,现在我们斜着看,请同学们观察斜向有没什么特征?
生10:左侧斜着一串数字加下来,会等于右下方的数字。
生11:对对对!右侧斜着一串数字加下来,会等于左下方的数字。
师:同学们发现得真快!
板演:斜行和。
PPT显示:
规律之美4:从杨辉三角中一个确定的数的“左(右)肩”出发,向右(左)上方作一条和左斜边平行的射线,在这条射线上的各数的和等于这个数。
师:从以上这4个规律,不同方向、不同角度看杨辉三角,“横看成岭侧成峰,远近高低各不同”在杨辉三角中展现得淋漓尽致,杨辉三角真的太美了!
师:现在老师带领同学们,一起来继续感受杨辉三角的魅力。请同学们把老师标记的每个斜行相加,观察和的特点。
生12:1,1,2,3,5,8,13...
师:看起来杂乱无章的这串数字,有什么特点呢?
生13:不断增大。
师:不错,有没有更特殊的规律呢?
生14:每个数字都是前两个数的和。
师:真棒!从第三个数起,任一数都等于前两个数的和,这是著名的斐波那契数列,即为兔子数列。
板演:规律5.斐波那契数列。
PPT显示:
规律之美5:斜看杨辉三角中各数的和,从第三个数起,任一数都等于前两个数的和。
【设计意图】斐波那契数列是数学文化史中趣味性很强的代表性范例,值得推广学习,从而引出斐波那契发现兔子数列的规律。
师:接下来,我们一起来了解有意思的斐波那契数列。
PPT显示:
中世纪意大利数学家斐波那契的传世之作《算术之法》中提出了一个饶有趣味的问题:假定一对刚出生的兔子一个月就能长成大兔子,再过一个月就开始生下一对小兔子,并且以后每个月都生一对小兔子.设所生一对兔子均为一雄一雌,且均无死亡.问一对刚出生的小兔一年内可以繁殖成多少对兔子?(如图1)
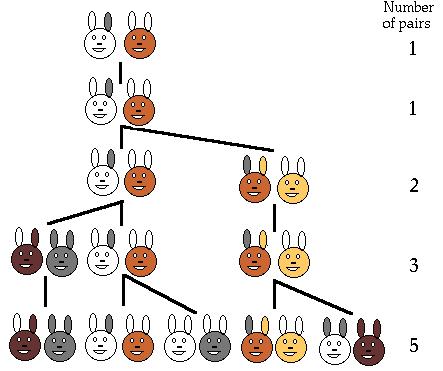
图1
兔子繁殖问题也可以从杨辉三角得到答案:
1,1,2,3,5,8,13,21,34,...
【设计意图】通过讲解斐波那契数列的来源,引导学生意识到数学来源于生活应用于数学的价值体现。同时,介绍数学家斐波那契热爱生活,善于观察生活,并将生活中的现象记录下来留下宝贵的精神财富,引导学生树立研究性学习的观念,渗透数学建模的思想。
师:杨辉三角除了我们发现的这5个规律外,还有一些神秘的规律,有待同学们课后去挖掘,同学们进入高中阶段也可以继续学习。
三、时光列车
师:同学们,我们了解了杨辉三角这么多内在的规律,发现杨辉三角不仅神秘,而且很美,这么有趣味性的杨辉三角是谁先发现的呢?它是怎么发展的呢?让我们通过微课的形式走进杨辉三角,了解它背后的故事,揭开它神秘的面纱。
微课展示:
(伴随着“高山流水”的背景音乐,杨辉三角的起源及发展的数学史娓娓道来)
首先介绍古代数学家贾宪,中国十一世纪上半叶(北宋)的杰出数学家。曾撰《黄帝九章算法细草》(九卷)和《算法古集》(二卷),都已失传。据《宋史》记载,贾宪师从数学家楚衍学天文、历算,著有《黄帝九章算法细草》、《释锁算书》等书。贾宪的主要贡献是创造了“贾宪三角”和“增乘开方法”。
然后介绍本课的主角——古代数学家杨辉,出生于南宋时期,1261年所著的《详解九章算法》一书中,辑录了三角形数表,称之为“开方作法本源”图(如图2),并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”。杨辉在所著《详解九章算法》、《开方作法本源》一章中作贾宪开方作法图,并说明“出释锁算书,贾宪用此术”。

图2
法国著名数学家、物理学家和哲学家帕斯卡,在13岁时(1654年)发现这一规律,所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年,比贾宪迟600年。帕斯卡在1665年出版《论算术三角形》,谈到“算术三角形”的构造和性质,并最早用数学归纳法证明了性质。
意大利数学家塔尔塔利亚的发现比帕斯卡要早100多年,比贾宪晚约500年。
最后引用学生熟知的现代数学家华罗庚的名言作为结束语:“数学是我国人民擅长的学科。我们祖国伟大人民在人类史上有过无比睿智的成绩。”
【设计意图】描述贾宪、杨辉成就的同时,详细介绍杨辉三角的来龙去脉,并告知今日认知的杨辉三角实际上是贾宪最早发现这一神秘的数学知识,一场美丽的误会充满了数学文化的趣味性,激发学生的学习兴趣。同时类比引出西方国家有关杨辉三角的史实,充分展现了中国古代数学家的辉煌成就,激发学生的民族自豪感,树立学好数学知识的信念。
师:同学们,我们通过搭乘时光列车,了解到杨辉三角的起源及发展,感受到我们民族在数学文化长河中取得的巨大成就,我们应该更有信心学好数学,继承和发扬我们数学的优势地位!
四、古为今用
师:同学们,杨辉三角如此美妙,它的用途肯定也不仅限于兔子繁殖问题,在生活中常常可以借助杨辉三角解决实际问题,请同学们看下这道题。
“纵横路线图”是数学中的一类有趣的问题。下图3是某城市的部分街道图,纵横各有三条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法?

【设计意图】通过生活中趣味性的问题,引发学生思考、动手操作实践,集思广益,学生得出结论。
师:审题完毕后,请同学们思考,你们能得到几种不同的走法呢?
生1:5种。
生2:6种。
师:好,我请答案为5种的同学到黑板上来演示,答案6种的同学稍后可以补充答案。
生上台演示。(一个同学演示5种情况后,另一个同学上台补充1种情况)
师:经过两位同学的实践操作,我们发现答案是 6。
师:如图3把图顺时针转45度变为图4,使A在正上方,B在正下方,然后在交叉点标上相应的杨辉三角数。B处的杨辉三角数与A到B的走法有什么关系?
生3:B处所对应的数6,正好是答案 6.
师:同学们想想,这里面可能隐藏了什么秘密呢?
生4:每个交点上的杨辉三角数,就是从A到达该点的方法数.
师:太棒了!我们发现原来生活中的路线问题也和杨辉三角有关,这个结论太赞了!
【设计意图】将生活实际中的路线问题,借助杨辉三角知识解题,自然过渡到本课所学新知,体现杨辉三角的应用价值。
变式:“纵横路线图”是数学中的一类有趣的问题。下图5是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法?

师:我们将题目中的三条路变为五条路,同学们可以课后试试。老师用杨辉三角尝试演示给同学们看,我们发现有70种。
师:原来,杨辉三角与纵横路线图问题有天然的联系,由此可见,杨辉三角在生活中无处不在,利用价值相当高。
【设计意图】变式题利用同样的方法,将路线图转化为图6,借助杨辉三角图7。借助学生外出旅游的经历,激发学生对本问题的兴趣,开动脑筋思考答案,动手操作得出结论。
五、提升思考
师:杨辉三角是不是纯粹欣赏,在考试中,是不是不会出现杨辉三角的考题呢?现在的中考高喜欢带上数学家一起来凑热闹,所以杨辉三角也是中高考试题的贵宾常客。接下来请同学们赏析这道中考题:
(2006年中考日照市卷第17题)德国数学家莱布尼茨发现了下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数):

根据前5行的规律,可以知道第6行的数依次是: .
师:同学们,看到这道题第一感受、反应是什么?
生1:杨辉三角,形状很像。
师:真棒!长相有点像是吗?我们一起看看这个数表的内在,每个数一样吗?
生2:数字的个数一样,但是每个数字不同。
师:非常好,只要类似,我们就可以用类比的方法解决它。我们现在要找到相同和不同之处,同学们有什么发现吗?
生3:数字都变成分数了,分子都为1.
师:既然都是1,我们可以怎么办?
生4:都把1先去掉。
师:很好!然后数字就一样了吗?
生5:分母好像有规律,有对称性。
师:然后呢?
生6:可以看作是变形的杨辉三角。
师:怎么变?
生7:去掉分子1后,分母的数字每行开头是1,2,3,4,5,而杨辉三角每行开头是1,1,1,1,1.
师:我们可以怎么处理?
生8:可以每行除以行数。
师:太棒了!
PPT显示:
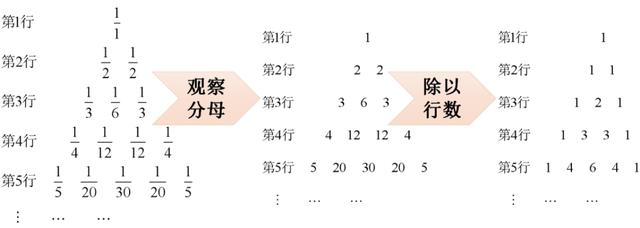
师:通过这两个步骤的变形,得到熟悉的杨辉三角。根据今天所学的规律,可以得到第6行数字是什么?
生:杨辉三角第六行数字为1,5,10,10,5,1,然后乘以行数,变为6,30,60,60,30,6,再分别把每个数取倒数。
【设计意图】借助本题引导学生认识杨辉三角在考试中可能出现的形式,同时引导学生掌握类比的思想和转化的方法。帮助学生先观察题中的单位分数三角形,逐步引导寻找单位分数三角形与杨辉三角的不同之处,层层递进,深入剖析,找出规律,借助杨辉三角的知识解决本题。
六、课堂总结
师:同学们,今天我们通过杨辉三角故事的品读,感受到杨辉三角内在的奥秘,体会到数学文化的趣味性,欣赏数学文化的美妙之处,并深深被数学文化的魅力所折服。同学们带着民族自豪感,阔步前行,继续探索数学的奥秘!
七、作业设计
1.查阅《杨辉三角》相关资料。
2.复习巩固《杨辉三角》的规律。
八、板书设计

相关链接>>
相聚于网络,相知因数学,相交为征文——第三届数学文化征文活动通知
第三届数学文化征文比赛评委简介
第二届数学文化征文比赛通知
第一届数学文化征文活动文章集锦
已发文章>>
001 莱布尼茨、二进制和伏羲卦图
002 美学视角下的数学教学 —— 读《数学的美与理》有感
003 数学基础与黎曼猜想 ——《数学简史:确定性的消失》读后思考
004 数学与文化并重 知识与兴趣同行 ——“算筹记数”教学思考
005 数学是多维度的艺术——读《数学家的眼光》有感
006 从掷骰子到阿尔法狗:趣谈概率
007 中学数学中分类思想的教学与拓展
008 守门的秘密
009 探数学文化,启数学之美——以高中数学《割圆术》为例
010 基于数学史视角的高中数学教学思考
011 我是怎样读《几何原本》的
012 相映成趣的两座数学桥
013 HPM视角下的数学概念教学——“平面直角坐标系”教学设计
014 极限定义新讲:动态定义与静态定义
015 把握思想方法,自主提升数学素养 ——读《让知识自然生长》有感
016 读北大张顺燕教授《数学的源与流》的几点收获
017 中国古代数学对“一带一路”沿线国家的影响
018 数学阅读锦上添花,实践成果领航数坛新征程
019 提高概率教学质量的几点思考
020 温故建构新知 论证生成巧思 ——三角形的中位线定理的探究
021 读《学好数学并不难》有感
022 体验经典证法 渗透数学文化 ——以“勾股定理(第一课时)”教学为例
023 数学文化 文化数学 ——融合数学文化的中考试题的品析与启示
024 善用数学文化 灵动数学课堂 优化育人途径
025 基于数学文化的高中数学教学的实践与研究
026 数学中的美—— 读《数学文化中的美育渗透》有感
027 利用“去分母”解一元一次方程教学设计
028 海伦公式
029 《镜花缘》中的数学“缘”
030 基于认知发展的数学理解教学 ——读《数学教学心理学》所思所行
031 做一位有文化的数学教师 ——读《数学教育中的数学文化》所感
032 向下扎根,追寻成长
033 运用读思达进行中考文化类试题解题策略研究 ——以2021福建、北京中考试题为例
034 2021年中考中的传统文化试题
035 数学文化阅读课——《圆周率的历史》
036 小学低年段课堂中渗透数学文化的思考 ——读张齐华老师《用文化润泽数学课堂》有感
037 五光十色的数学之《数学及其历史》观后有感
038 小折纸,有大历史 ——可以写入教材的“一刀剪”最大精确五角星折法
039 新高考改革背景下数学文化情境试题的考查研究 ——兼评2020年高考数学文化试题
040 浅谈《怎样解题》对教学的指导
041 如何让数学文化浸润常态化课堂教学——读顾亚龙《以文“化”人》专著有感
042 中学教材和中考命题中的数学文化探析
043 在初中数学教学中渗透民族文化自信
044 初中数学教学中数学文化的渗透策略
045 第二章 探索图形的规律——火柴棍里的数学文化课堂实录
046 浅谈数学文化在小学数学课堂教学中的渗透
047 核心素养视角下数学活动的实施策略探究
048 基于数学史视角的初中数学教学思考——读《数学文化漫谈》有感
049 读《张奠宙数学教育随想集》有感
050 读浙大蔡天新教授《数学传奇》有感
051 HPM视野下《一元二次方程概念》教学实录与设计分析
052 探寻单位“1”下的直观模型 ——读《度量:一首献给数学的情歌》有感
053 数是现实与想象的结合 ——读《度量:一首献给数学的情歌》的想象
054 基于数学之美的小学数学命题设计
055 “将军饮马”问题的前世今生
056 一次“数学文化”答题活动的题目设计






