本文既可作为老少皆宜的休闲文章来看,也可作为本科生速成期末考试的灵丹妙药(笑)

牛顿
什么是微分方程呢,我们将通过几个实例带大家了解它。话不多说,让我们开门见山:
首先映入眼帘的是这样一个实际问题:
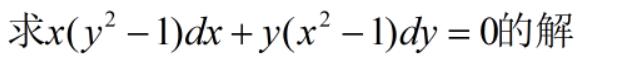
大家一眼看上去感觉很迷茫:两个未知量xy,还有两个微元小量 dx dy,然后是一个等式连接的,求解?是求谁的解呢?
这就是微分方程的一种形式之一,我们究竟是要干什么呢?我们要做的工作是把这个抽象的等式变成 y=f(x),这一求y=f(x)的过程就称为求解:


但是有两个未知量xy,还有微元小量 dx dy啊,怎么处理就能把变成y=f(x)这种形式的方程组呢?真是让人感到匪夷所思。不过,聪明的前人经过了多次失败和试错,终于是找到了办法:
第一步,把它倒过去

然后:分离变量:

我们知道:

如果你懂最基本的微积分,你就会看懂这个基本的微分公式(不懂可以看笔者之前的文章)

所以,我们可以得到:

c2-c1也可以,无所谓的,甚至加起来也无所谓,因为两个c都是不确定的常数
把右边ln加到左边,根据ln乘法的性质,可以得到:

我们现在得到这样一个东西:

然后你问了,你不是说必须得到y=f(x)这种形式吗?

说得不错,于是我们继续分析。

当x=±1的时候,C3=0,y是任意的。

当x≠±1的时候:

我们终于等式变函数,使得y和x金蝉脱壳了。对于y=f(x)这样的一元函数,我想大家已经了解其中的意义了吧?

我们把这两种情况下的解合到一块儿,就是所谓的通解,通解的意思就是所有情况的解。
我们发现y取决于C3,如果C3=0,不论x取什么值,y都等于0。如果C3取个1,就有别的解了,如果只把x等于±1看做上面那个等式的一种解,也是一种独立的情况。
我们把某个特定情况(比如被初始条件限制)下的方程解叫“特解”。它只是特定情况下的解,是被通解包括进去的。
这就是通解和特解的大致概念。我这个人向来不喜欢专业术语,大家知道意思就行了,正如我的一位朋友所言:认知皆模型。我们要透过现象看本质。