近年来,空间重构中的小方块立体拼合成为公考新宠。因为面对这种题,考生必须具备一定的空间思维能力,能考查出考生的实际水平。不像六面体,考生只要掌握一定的解题技巧,即使没有丝毫空间想象能力,也能把题作对。
对于空间思维较弱的同学,这种题着实让人头疼,今天华小图就带大家一起总结一下答题的方法。
方法一:数数量
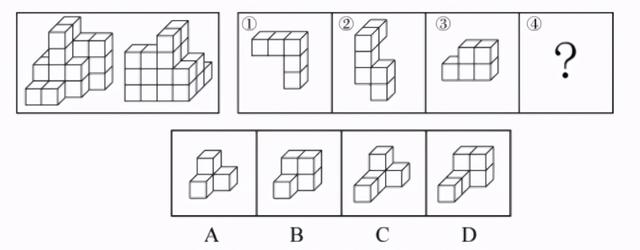
对于一些简单题型,只要数一数给定的拼合后的图形一共有多少块,减去已知图形方块的数量,剩下多少跟选项匹配即可,即使不能直接找到最终的答案,也能排除一部分选项。比如,给出的立体图形一共有30块,已知的①、②分别是12块、10块,那正确选项只能是8块,不是的都可以排除。以下题为例,题中左侧立体图有22块,①5块、②6块、③5块,④应为6块,只有D项。
【例1】下图多面体可拆分为①、②、③和④共4个多面体的组合,问下列哪一项能填入问号处?
方法二:最大跨度法
图形跨度越大,能放置的位置就越局限,因此我们可以先把跨度最大的图尝试放置,越小的块越后放。如例2所示,四个小图中,图③占4格,为跨度最大的一个,其只能放在下数第一和第二层。不管放在哪,都不可避免的会将剩余部分分割成两小块或一小块的小零件,这样的小零件在其他图中是不存在的,因此图③可以排除,能拼成左侧立体图的是①、②和④,至于到底如何拼,不需要考虑。
【例2】左图所示立体图形,可以由哪三个图形组成?

方法三:俯视减法
对立体图形做俯视图,标记每个纵向上小块的数量,再将已知项的数量在俯视图上做减法。结合一道例题理解。
【例3】左图给定的是由相同正方体堆叠而成多面体的正视图和后视图。该多面体可以由①、②和③三个多面体组合而成,问以下哪一项能填入问号处?

【解析】左侧立体图形做俯视图并标记每列小块数量得到图一;①每纵列小块数量是2、2、2、1,在图一上第一行数量恰好接近,如图二做减法;②每纵列小块数量为3、2、2、1,只有左侧一列有足够的块可减,如图三做减法;最终生成图四,即答案项为4个1 1个2的布局,只有B项符合。

当然还有一些图靠我们简单的看特征块或凹凸位置就可以锁定选项,在这里不一一总结。对于空间拼合,还是需要大家结合我们的方法,多做练习,培养一定的空间思维能力。建议大家买一个索玛立方,没事的时候拼一拼,锻炼自己的空间思维能力。
没有什么是一劳永逸的,尽早备考,踏实努力。明天的你必将感谢今天努力的自己。
,




