滤波器作为电子系统中十分常见的工具,在信号处理中占有重要地位。本文将对两种典型的滤波器原理进行分析,并借以理解其他各式滤波器。 滤波器是一种选频装置,可以使信号中特定的频率成分通过,而极大地衰减其它频率成分。在测试装置中,利用滤波器的这种选频作用,可以滤除干扰噪声或进行频谱分析,从而达到“去除杂波,选择信号”的作用。 广义地讲,任何一种信息传输的通道(媒质)都可视为是一种滤波器。因为,任何装置的响应特性都是激励频率的函数,都可用频域函数描述其传输特性。因此,构成测试系统的任何一个环节,诸如机械系统、电气网络、仪器仪表甚至连接导线等等,都将在一定频率范围内,按其频域特性,对所通过的信号进行变换与处理。 滤波器可分为低通滤波器、高通滤波器、带通滤波器、带阻滤波器和全通滤波器五类。本文将分析介绍低通滤波器和高通滤波器这两种常用滤波器原理,以求触类旁通,同时掌握所有五种滤波器。 【低通滤波器】 所谓低通滤波器(LPS:low pass filter)是允许低频讯号通过,而不允许高频讯号通过的滤波器。容许低于截止频率的信号通过, 但高于截止频率的信号不能通过的电子滤波装置。以一阶低通滤波器为例,其组成与响应曲线如下: 截止频率:f=1/(2*Pi*R*C) ,
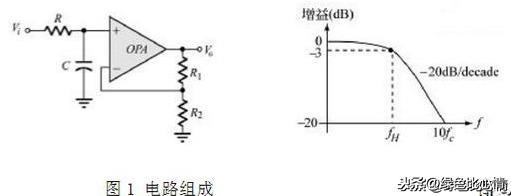
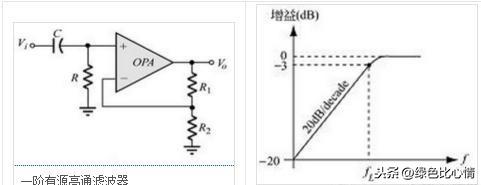
频率低于fh时,增益为电压增益;频率高于fh时,增益的衰减斜率为每10倍频率20dB。 由此即可滤除频率高于fh的信号,只保留低于fh的部分。 为帮助更好地理解,举一个例子:一个固体屏障就是一个声波的低通滤波器。当另外一个房间中播放音乐时,很容易听到音乐的低音,但是高音部分大部分被过滤掉了。类似的情况是,一辆小汽车中非常大的音乐声在另外一个车中的人听来却是低音节拍,因为这时封闭的汽车(和空气间隔)起到了低通滤波器的作用,减弱了所有的高音。 对于高于fh的频率,信号按该频率平方的速率下降。在频率fh处,阻尼值使输出信号衰减。可以级联多个这样的滤波器部分来得到一个更高阶的(更陡峭的转降)滤波器。假定设计要求一个截止频率为10kHz的四阶贝塞尔(Bessel) 低通滤波器。根据参考文献1,每部分的转降频率分别为16.13及18.19 kHz,阻尼值分别为1.775及0.821,并且这两个滤波器分区的高通、带通和低通系数分别为0、0与1。您可以使用这两个带有上述参数的滤波器部分来实现所要求的滤波器。截止频率为输出信号衰减3 dB的频率点。 【高通滤波器】 高通滤波器允许信号中的高频分量通过,抑制低频或直流分量。是一种让某一频率以上的信号分量通过,而对该频率以下的信号分量大大抑制的电容、电感与电阻等器件的组合装置.一阶高通滤波器原理图及幅频特性曲线如下: 类比低通滤波器,我们不难得出:假设截止频率为fh,则频率高于fh时,增益为电压增益;频率低于fh时,增益的增长斜率为每10倍频率20dB。 换句话讲,高通滤波器可滤除低于某一频率的信号,只保留高于这一频率的部分。
【带通滤波器】 带通滤波器是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到极低水平的滤波器,与带阻滤波器的概念相对。一个模拟带通滤波器的例子是电阻-电感-电容电路。 这些滤波器也可以用低通滤波器同高通滤波器组合来产生。将上述两种典型滤波器加以组合,过滤掉低于fl的部分和高于fh的部分,则剩下的就是频率介于fl与fh之间的带通部分。 【带阻滤波器】 带阻滤波器(简称BSF)是指能通过大多数频率分量、但将某些范围的频率分量衰减到极低水平的滤波器,与带通滤波器的概念相对。 类比上面带通滤波器,不难看出,带阻滤波器同样可视为高通和低通滤波器的叠加——即滤除频率低于fh的部分和高于fl的部分,只保留剩下的部分(右图中的通带部分)。 【全通滤波器】 全通滤波器是指在全频带范围内,信号的幅值不会改变,也就是全频带内幅值增益恒等于1。很显然,当低通滤波器与高通滤波器截止频率相等时,即fl=fh时,在全频域内信号幅频特性曲线均无下降,为一条平行于频率轴的直线。此时为全通状态。 【总结】综上所述,在了解了高通滤波器和低通滤波器的原理之后,我们就可以很轻易地理解所有滤波器的相关性质。只要牢记这两种滤波器原理,其他滤波器也不在话下。