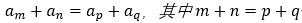(一)基本概念
整数a能被非零整数b整除,称a为b的倍数,b为a的因数。若两数的最大公因数为1,则称这两个数互质。
(二)计算方法
1、分解质因数法
2、短除法(求最大公倍数时,用几个数的公因数去除每个数,再用部分数的公因数去除,把不能整除的数移下来,除到所有商两两互质,然后把所有除数和商相乘)
整除
题目中出现了分数、百分比、比例等数据形式的时候,要考虑是否用整除。
(一)整除的判定
|
分类 |
对应数字 |
判定方法 |
示例 |
|
有尾数 |
2,5 |
末一位能被2或5整除 | |
|
4,25 |
末两位能被4或25整除 | ||
|
8,125 |
末三位能被8或125整除 | ||
|
看和 |
3 |
各位之和是3的倍数 | |
|
9 |
各位之和是9的倍数 | ||
|
看差 |
11 |
奇位数数字之和与偶数位数字之和做差,差能被11整除 |
1639,奇数位之和为4,偶数位之和为15,相差11 |
|
7,11,13 |
末三位数字与剩下数之差能被7,11,13整除 |
1005928,末三位为928,剩余为1005,做差为77,能被7或11整除 | |
|
合数 |
6,12等 |
能同时被除数分解后的互质因数整除 |
12=3*4,2724既能被3整除,又能被4整除,则能被12整除 |
(二)整除的性质
1、可传递性:若A能被B整除,B能被C整除,则A能被C整除。
2、可加减性:若A能被C整除,B能被C整除,则A B、A-B能被C整除。
3、甲/乙=m/n,则甲 乙是(m n)的倍数,甲-乙是(m-n)的倍数,其中m,n互质
例1:现有肉兔和宠物兔两种兔子共计2200只,所有兔子的毛色分为黑、白两色。肉兔中有87.5%的毛色为黑色,宠物兔中有23%的毛色为白色,那么毛色为白色的肉兔至少有多少只?
(87.5%=7/8,则肉兔总数为8的倍数,宠物兔为100的倍数,2200为100的倍数,所以肉兔也为100的倍数,8和100的最小公倍数为200,则肉兔最少200只,白色肉兔最少为25只)
例2:某市举行业务技能大赛,其中东区参赛人数占总人数的1/5,西区参赛人数占占总人数的2/5,南区参赛人数占总人数的1/4,其余的为北区的参赛人数,结果东区参赛的1/3获奖,西区参赛人数的1/12获奖,南区参赛的1/9获奖,已知参赛人数超过100人,不到200人,则参赛总人数为
A、160 B、120 C、140 D、180
(南区获奖人数=总人数*1/4*1/9,则总人数至少为9的倍数,选项中只能选D)
例3:某单位从理工大学、政法大学和财经大学,总共招聘应届毕业生300多人,其中从理工大学招聘人数是政法大学和财经大学之和的80%,从政法大学招聘的人数比财经大学多60%,问该单位至少再招聘多少人就能将从这三所大学招聘的应届生平均分配到7个部门?
A、6 B、5 C、4 D、3
(设财经招聘x,则政法为1.6x,理工为52x/25,则总招聘人数为2.6x 52x/25=117x/25,x=3*25时,总人数为三百多人,为351,351/7=50……1,则再招6人)
平均数
(一)平均数的简便计算
当一组数据在某个数值附近上下波动时,可以此数据为基准,通过计算每个数据与基准的差距来确定平均数
举例:求93、96、89、91、87、94、88、98这八个数字的平均数
(观察发现,均在90附近上下波动,每个数字相对于90的差值分别为3、6、-1、1、-3、4、-2、8,则所求平均数为90 2等于92)
等差数列
(一)基本公式
|
分类 |
公式 |
|
通项 |
等差数列通项 |
|
对称 |
等差数列对称性 |
|
平均数 |
平均数=(首项 末项)/ 2 项数为奇数时,平均数=中项 项数为偶数时,平均数为中间两项之和的一半 |
|
中项 |
n为奇数,则奇数项之和 - 偶数项之和 = 中项 |
|
一般求和 |
等差数列求和公式 |
|
中项求和 |
和=中项*项数 (n为奇数) |
|
平均数求和 |
和=平均数*项数 |
(二)特殊数列求和
|
数列名称 |
和 |
|
奇数列 1,3,5,...(2n-1) |
n^2 |
|
偶数列 2,4,6,....2n |
n^2 n |
求解不定方程
两个方程三个未知数,求三个未知数之和,可以令某一个未知数为0,求解剩下两个未知数,然后求和。
,