同类项指的是所含字母相同,并且相同字母的指数也分别相同的项。同类项要注意以下几点:(1)判定两个代数式是否是同类项,需要满足两个条件,所含字母相同,并且相同字母的指数相同,同时具备两个条件,缺一不可;(2)同类项与系数无关,与字母的排列顺序无关。
把多项式中的同类项合并成一项,叫做合并同类项,合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变,合并同类项的根据是乘法分配律的逆运用,可以利用划记法进行标记。

类型一:同类项的概念
根据同类项的概念求解相关参数问题。
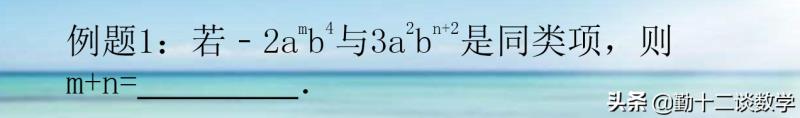
分析:直接利用同类项的概念得出n,m的值,即m=2,n 2=4,得到m=2,n=2.
这类题目比较简单,题目中明确说明两个单项式是同类项,根据同类项的概念求解即可。有些题目不会明确说明,比如说两个单项式可以合并,两个单项式的和也为单项式等等,遇到这样的说法也要知道两个单项式为同类项。
类型二:合并同类项
在合并同类项时,注意将所有的常数项都是同类项,合并时把它们结合在一起,运用有理数的运算法则进行合并,合并同类项时可以利用划记法。
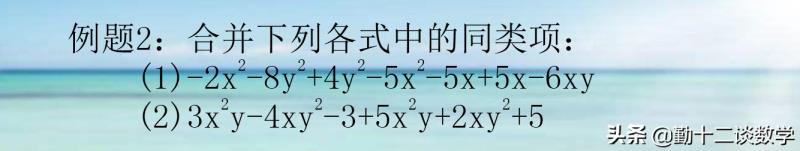
在进行合并同类项时,可按照如下步骤进行:第一步:准确地找出多项式中的同类项(开始阶段可以用不同的符号标注),没有同类项的项每一步保留该项;第二步:利用乘法分配律的逆运用,把同类项的系数相加,结果用括号括起来,字母和字母的指数保持不变;第三步:写出合并后的结果。
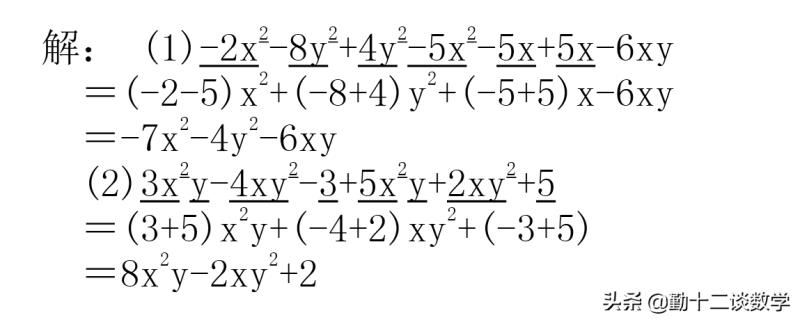
在刚开始练习时,可以全部选择加法进行运算。

类型三:化简求值题
先化简,再求值,注意格式问题。
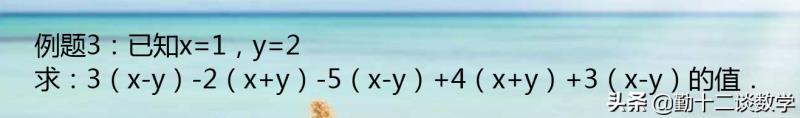
分析:不要一下子将所有的括号都去掉,可以先将x-y和x y看作一个整体,最后再去括号化简。
解:原式=3(x-y)-2(x y)-5(x-y) 4(x y) 3(x-y)=(x-y) 2(x y)=3x y;
当x=1,y=2时,原式=3×1 2=5.

类型四:“无关”与“不含”问题
这类题目主要考查了整式的加减,正确合并同类项是解题关键。
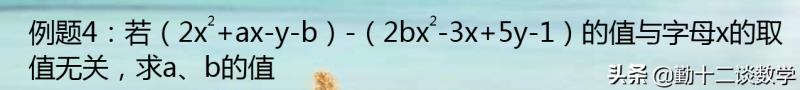
分析:直接去括号合并同类项,再利用与字母x的取值无关,得出关于a,b的等式,求出答案即可.
解:解:(2x^2 ax-y-b)-(2bx^2-3x 5y-1)=2x^2 ax-y-b-2bx^2 3x-5y 1=(2-2b)x^2 (a 3)x-6y-b 1,
则2-2b=0,a 3=0,
解得:b=1,a=-3.





