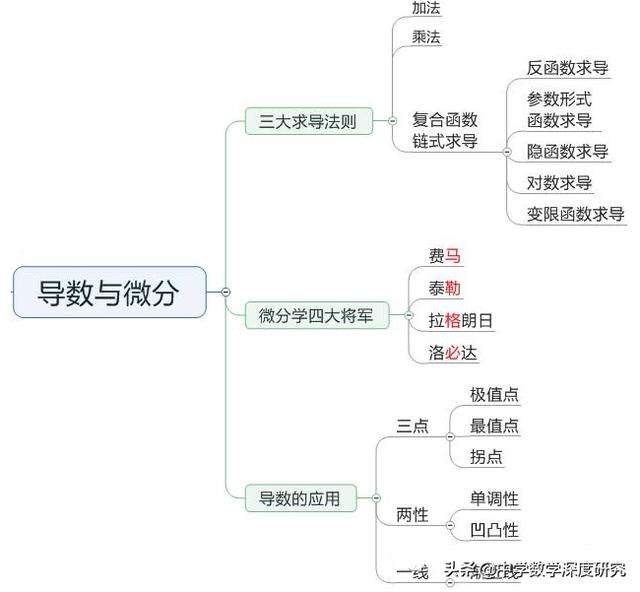
我们知道很多著名的科学公式,其实都是一个个人名,比如欧姆定律、费马定理、欧拉公式等,科学家们凭借伟大的才华和直觉发现了这些定理,后人将这些定理冠以其姓名,以示纪念。
殊不知在这些堪称经典的以发现者命名的公式里,还混进了一个滥竽充数的人...,此人本身毫无才华,花了一点钱,从真正的科学家手里,偷来了公式的命名权。这个受到玷污的公式叫做洛必达法则,这个公式背后的厚脸皮人名字叫做——洛必达。

十七世纪末,牛顿和莱布尼兹分别创立微积分,数学领域迎来高速发展的"春天",也迎来一大批优秀的数学家,其中,伯努利家族在欧洲享有盛名,约翰·伯努利(1667-1748)和他的哥哥雅各布·伯努利号称"数学双雄",他儿子丹尼尔·伯努利就是流体力学中"伯努利原理"的发现者,当然,约翰·伯努利最大的成就,是培养了"欧拉"这位史诗级的大数学家。

而洛必达(1661-1704)出生在一个权势极高的贵族家庭,翻云覆雨令人畏惧,来访之人无不对这位公子赞不绝口,受宠溺的程度堪比网红明星,渐渐地他就感觉自己能上天了,能和太阳肩并肩了,他需要在别人面前说一口流利的拉丁文,来体现自己高雅的品味和横溢的才华。
不幸的是,高傲的他从来不肯用功,学了四年毫无效果。但是他觉得自己是如此的高明而神圣,压根不用费劲,知识就会自动流进他的脑子里...,于是整天依旧不学无术游山玩水泡妹子。
他的品格如此差,让老师叹为观止,但是背景却如此硬,让老师敢怒不敢言,
挥舞的教鞭总是在心里,狂跩的粉笔头总是在梦里。
四年之后,一脸辛酸的老师回家了,因为洛必达决定不当语言学家了。他要改当一名骑士,当骑士不用动脑子,而且那铠甲与铁剑发出的凛冽寒光,岂不是一种更极致的装逼?陌生人的灼热目光和红肿膝盖,是他想要的。
据记载,他精心选了一匹马,那马当即用后腿踹了他一脚,直接导致他躺了一个月,康复之后的他,觉得还是先不要学骑马了。先学练剑吧,就在这时,军队的长官发现了一个令人悲伤的事情,他的眼睛看不清距离自己十步以外的任何东西,原来他是个高度近视,这辈子与骑士无缘了。

过了很久以后,洛必达已经30岁了,还是没有正经事可以干,任何高质量的逼都还没有装过,觉得很亏,他急需一个令人折服的装逼技巧。
他将目光瞄向了,古老而神秘的数学,在聚会上摊几个高深的数学公式,效果一定是极好的,他如是想着。后来经过努力研究,他真的憋出了几个数学公式,准备赌一把,去点亮人生中最关键的装逼时刻。
机会出现了,一场贵族聚会上,他遇到了声名显赫的数学家伯努利,我们的主人公洛必达一个勾手,拦住了伯努利,当场就把自己的公式撂给了对方,伯努利是个有真才实学的人,
他诚恳地对洛必达说:"这些都是最基本的数学公式,任何中学生都应该学过。"
一旁的伯爵与贵妇,对洛必达露出了轻蔑嘲笑的白眼,那一瞬间他整个人都褪色了,心里的凄冷,就像一台刚刚发现自己不能发电的缝纫机那样令人心疼。
洛必达觉得伯努利确实厉害,造诣不知比自己高到哪里去了,在1695年,他给约翰·伯努利的信说:我希望你,能在才智上帮助我,我也将在财力上帮助你,我提议将每年给你三百个里弗尔(相当于136千克白银),并外加两百个里弗尔作为你之前给我辅导的额外报酬,要求你从现在开始,定期给我一些你的研究成果和最新发现,但是这些成果你不能告诉其他人,至于报酬,我还会不断增加数量。
他把伯努利带回了家,让他给自己教数学,伯努利才讲了一点,他就感觉脑子差点爆炸了。他跟伯努利坦白,我只是想装个逼而已,我给你一磅银子,你给我一个全新的数学公式,怎么样?
约翰·伯努利刚结婚,正是用钱之际,如果拒绝这位贵族的要求,对他来说确实是不智的,既然这样,何不各取所需,再说这笔报酬的确看得出洛必达的"诚意",于是约翰·伯努利定期寄给洛必达他的新发现。
洛必达拿着买来的高级公式,又到贵族场所里显摆,而这次换来的是一些惊叹和赞美,甚至有人称他为"法国杰出的数学家",食髓知味的他,决定再接再厉,要从伯努利那里拿到更厉害的公式。

他写信给伯努利:"我给你300磅银子,来买你今年所有的学术成果,这些成果不能透露给任何人,否则你等着,我让家里的人来治你。"
伯努利以为他又是为了装逼,还是没多想,再次欣然同意了。这一年之内,伯努利作出了许多重大的成就,包括一个在微积分领域非常重要的公式,一并卖给了洛必达。
万万没想到,洛必达收到伯努利这些成果后,立马着手研究,并加以整理,一年后,洛必达把整理出来的一些内容著成了一本书——《无穷小量分析》,这也是第一本系统介绍微积分的书籍。在前言中,他欲与牛顿试比高,写道:"牛顿曾经百思不得其解的难题,被我解决了。"

其中那个重要的微积分公式,被大众广泛接受,随着时间的推演逐渐有了一个广为知晓的名字——洛必达法则:
我们可以知道,在运用洛必达法则之前,首先要完成两项任务:一是分子分母的极限是否都等于零(或者无穷大);二是分子分母在限定的区域内是否分别可导。如果这两个条件都满足,接着求导并判断求导之后的极限是否存在:如果存在,直接得到答案;如果不存在,则说明此种未定式不可用洛必达法则来解决;如果不确定,即结果仍然为未定式,再在验证的基础上继续使用洛必达法则。
比如0^∞,∞^0, ∞/∞,1^∞, ∞-∞等等,一般都可以化为0/0型,两个函数的极限都趋于一个点,那么从他们曲线上来看,该点处他们函数极限值的比值,其实就是他们在此处切线斜率之比,也就是求导后的函数,在此处的值之比。

他本人因此受到万人敬仰,成了交口相传的自学成才佳话,对数学的贡献之大,
以至于受到各国元首的接见,还被选入法国科学院。那一刻,他终于沐浴到,成为万人拥戴的红太阳的骄傲感觉,不久之后,他就因为纵欲过度死了,此时他仅43岁。
在他去世后,伯努利发声:"我才是'洛必达法则'的真正创立者,只是当年洛必达给了不菲的报酬我才卖给了他,这个法则应该更名为'伯努利法则'"!但伯努利的言论却遭到了人们的质疑:"你当初为了蝇头小利背叛了数学道德和良知,现在发声也不过只是为了自己的利益而已。"