编码单位和未编码单位定义实验设计中的因子水平。例如,您要确定哪种压力设置与底漆类型的组合能够获得最优的涂层附着力。实验中的低设置(压力 = 310,底漆类型 = 一)由采用编码单位的 -1 标识,高设置(压力 = 380,底漆类型 = 二)由采用编码单位的 1 标识。
注:如果实验中有中心点处实验,则中心点的编码单位用0标识


默认情况下,Minitab 使用编码单位来执行分析。
未编码与已编码的互相转换在Minitab 19中的路径:统计-DOE-显示设计


在“显示设计”的因子单位改选为“已编码单位”


我们也可以手动计算实现编码和未编码的转换(详见蓝宝书P505)。
编码值=(未编码值-M)/ D
未编码值=M D*编码值
其中,中心值M=(高 低)/ 2
板间距D =(高-低)/ 2
我们以已编码工作表第一行的加热温度0为例,把它转换为未编码值(加热温度高水平860,低水平820)。
M=(高 低)/ 2=(860 820)/ 2=840
D=(高-低)/ 2 =(860-820)/ 2 =20
未编码值=M D*编码值=840 20*0=840
DOE中的以编码系数与未编码回归方程在实验设计的分析结果中,我们会看到以下两个输出:


“已编码系数”表,可以帮助我们用来确定哪些项对响应具有统计意义显著的效应。要确定响应与模型中每个项之间的关联在统计意义上是否显著,请将该项的 P 值与显著性水平进行比较以评估原假设。原假设声明该项的系数等于零,这意味着该项与响应之间没有关联。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在实际上不存在关联时得出存在关联的风险为 5%。
P 值 ≤ α:关联在统计意义上显著
如果 P 值小于或等于显著性水平,则可以得出响应变量与项之间的关联在统计意义上显著的结论。
P 值 > α:关联在统计意义上不显著
如果 p 值大于显著性水平,则无法得出响应变量与该项之间的关联在统计意义上显著的结论。您可能希望重新拟合没有该项的模型。
如果多个预测变量与响应在统计意义上没有显著的关联,则可以通过删除项(一次删除一个)来简化模型。
在该“已编码系数”表中,我们看到每项的P值都是小于0.05,也就是说这些项都是显著的,需要在最终模型中保留。我们也可以借助效应Pareto图得到相同的结论。

而我们在上面看到的另外一个输出“以未编码单位表示的回归方程”其实是根据“已编码系数”表转换而来。下面我们来说明这两者的转换过程。
在转换之前我们首先来理解一下“已编码系数”表中的各项系数是怎么来的。

系数用于描述模型中的项和响应变量之间关系的大小和方向(要最小化各项之间的多重共线性,所有系数都需采用编码单位。)一个项的系数表示在其他项保持恒定时,与该项中一个编码单位的增长相关联的平均响应的变化。系数的符号表明项与响应之间关系的方向。
系数的大小是效应大小的一半。效应表示当因子水平由低变高时预测平均响应中的变化。也就是说各项的系数=(该项因子在高水平的响应均值-该项因子在低水平的响应均值)/2.,其中“常量项的系数大小为所有响应值(C9列)的平均值。那么下面我们先来求一下“常量”项的系数。

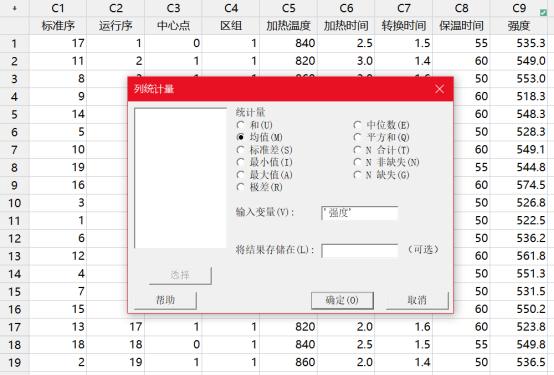


而各因子项和因子交互作用项的系数就是对应项的效应值一半,比如,在该“已编码系数”表中加热温度项的效应值20.04(加热温度的效应值是以下工作表中红色列对应的强度均值-绿色列对应的强度均值)。
( ( ( ( ( ( ( 553 548.3 ) 549.1 ) 574.5 ) 536.2 ) 561.8 ) 551.3 ) 536.5 ) / 8 - ( ( ( ( ( ( ( 549 518.3 ) 528.3 ) 526.8 ) 522.5 ) 531.5 ) 550.2 ) 523.8 ) / 8=20.0375
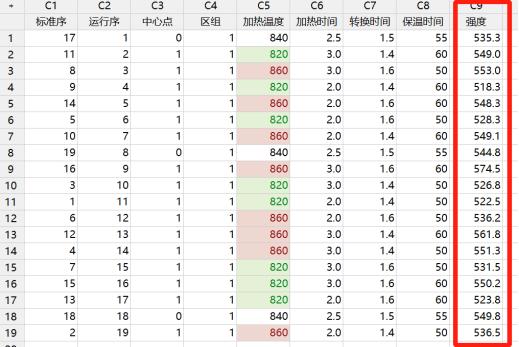
效应20.04的一半,所以加热温度的系数则为10.02,其他项的计算也是如此,不再赘述。
理解了效应和系数的计算后,我们现在来把“已编码系数”表转换为“以未编码单位表示的回归方程”。

强度 = 541.63 10.02 * ( 编码的加热温度 ) 8.44 * ( 编码加热时间 ) 5.56 * ( 编码保温时间 ) 3.56 * ( 编码加热时间 * 编码保温时间 )
其中编码的加热温度=(温度值-M)/ D, 具体计算过程见本文前面内容。所以:
强度=541.63 10.02 * [ ( 加热温度-840 ) / 20 ] 8.44 * [ ( 加热时间-2.5 ) / 0.5 ] 5.56 * [ ( 保温时间-55 )/5 ] 3.56 * [ ( 加热时间-2.5 ) / 0.5 ] * [ ( 保温时间-55 ) / 5 ]
手算结果为:强度=213.23 0.501加热温度-61.44加热时间-2.448保温时间 1.424加热时间*保温时间
与Minitab的“以未编码单位表示的回归方程”结果比较一下

如果你想更好的理解DOE中的分析结果,找个例子手算看看,会加深你的印象。当然有Minitab的帮助你也可以直接忽略计算过程。学习了DOE中的已编码和未编码,那你知道编码的作用吗?
,




