这段时间,一直在教学“多边形的面积”:平行四边形的面积、三角形的面积、梯形的面积,最后是组合图形的面积。前三种都用的是“转化法”,把新知转化为旧知来推导公式的,例如,把平行四边形转化为长方形、把三角形和梯形转化成平行四边形等;而组合图形是用分割法把图形分成几个学过的图形来解决。其中,出错最多的是有关三角形和梯形的面积方面的习题。

1.求面积总是忘记“÷2”
三角形和梯形在教学面积公式的时候,都是运用“拼接法”进行推导的:将2个完全一样的三角形,拼成一个等底等高的平行四边形,由此推导出一个三角形的面积公式是——平行四边形的面积÷2,即三角形的面积=底×高÷2;同样,把2个完全一样的梯形,拼成一个等高的平行四边形,此时平行四边形的底即梯形的上底与下底之和,因此,一个梯形的面积=平行四边形的面积÷2,即梯形的面积=(上底+下底)×高÷2。
在教学时,我特别在意学生动手操作活动,还专门让他们准备了完全相等的两个三角形(直角、锐角、钝角、等腰直角三角形等),准备完全相等的梯形(一般、直角、等腰梯形等),然后,让他们拼一拼,说一说,并且找学生到黑板前边操作演示,边推导公式。在课堂里,孩子们都很清楚,两个完全相等的三角形拼成了一个平行四边形,所以一个三角形的面积就得用平行四边形的面积除以2;两个完全相等的梯形拼成了一个平行四边形,因此一个梯形的面积就是平行四边形的面积除以2。
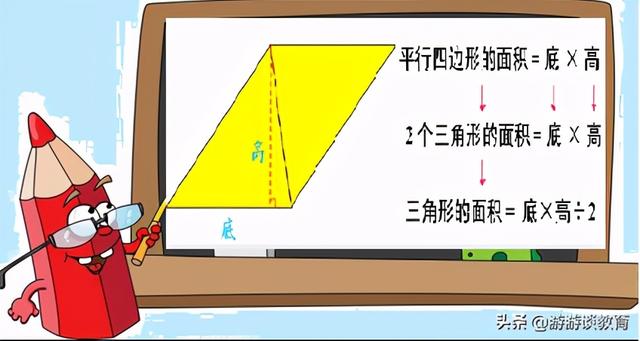
推导公式的时候,我也特别强调要“÷2”。但是,在做作业的时候,总有一些孩子忘记“÷2”,把三角形或梯形的面积均算成平行四边形的面积了。我分析了一下,可能有这两个原因:一是有的孩子喜欢列分步算式,求面积不代入公式,而是先算平行四边形的面积,再÷2,这就导致计算过程中容易漏掉“÷2”这一步;二是在推导三角形面积公式的时候,是把2个三角形拼成一个平行四边形来计算的,有的孩子就对平行四边形印象深刻,因此导致忘记“÷2”。
对此,我要求学生在做题的时候,一定要把面积公式写出来,然后把数据代入公式里计算,这样就不容易漏掉“÷2”了,等以后用熟练了,再脱离公式直接计算。

2.求高或底(或者上底、下底),忘记“×2”
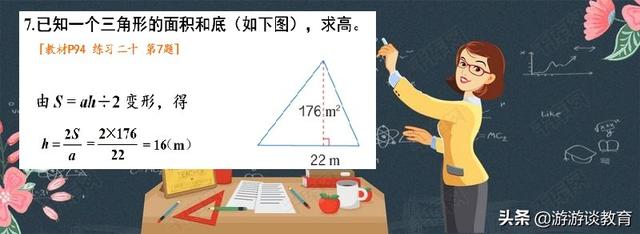
在练习题中,并不是所有的题都是套用面积公式直接算出的,有不少题是变形题,根据三角形的面积和底求高,或者根据梯形的面积、高和上底,求下底。例如:已知一个三角形的面积是176平方米,底是22米,高是多少米?此题可以用方程解,也可以用算术法来计算。
用算术法计算时,就得先把三角形面积还原成等底等高的平行四边形面积,然后才能用面积除以底,求出高的值。学生在做这类题时,有的忘记“×2”就直接用三角形面积÷底,显然是不对的。所以,在此要强调,必须先×2,得到等底等高平行四边形面积之后,再除以底。
又例如:已知一个梯形的面积是15厘米²。它的上底是4.5㎝,高是3㎝,下底是多少㎝?
此题可以用方程解决,也可以用算术法算出。用算术法时同样要用梯形面积×2,还原成平行四边形,再用平行四边形面积÷高=底,因为平行四边形的底=梯形的上底+下底,所以,梯形的下底=平行四边形的底-梯形的上底。
为了让学生记住“×2”,除了加强练习之外,教师还应将三角形和梯形结合起来进行归纳:三角形和梯形有相似之处,在求面积时都要“÷2”(都是用两个相同的图形拼成平行四边形,求一个图形的面积就要÷2);在知道面积和底(或上底、下底)求高时,都得先用面积×2,得到平行四边形,再求高。这样分类归纳之后,更有条理性,孩子们记忆就会清楚一些。

3.要以“平行四边形”为媒介
通过前两点,我们可以看到三角形和梯形在推导面积公式时,都是用平行四边形为媒介,因此,一定要给学生充足的时间动手操作,亲身体验三角形、梯形转化成平行四边形的过程,这样,在后面做题的时候,他们的脑海里就会浮现动手拼图的具体画面,能够帮助他们解决抽象的实际问题。
除此之外,可以让学生自己用思维导图描绘出长方形、平行四边形、三角形、梯形之间的相互联系。

为了拓展学生思维,可以在练习题中多找一些各种各样的变形题来做,见的多了,练得多了,自然就能应付各种考试题目,熟能生巧嘛。
,




