1880年的几个月中,整个美国陷入到“15 谜题”游戏的狂热中。1880 年 3 月 12 日,美国堪萨斯州当地一家媒体撰文称:“15 谜题风靡全国各个城市,人们不眠不休,为之疯狂。”之后,对该游戏的狂热又传到了欧洲、澳大利亚和新西兰。

图丨“15 谜题”要求玩家移动标着数字的卡片,目标是让 15 个数字有序排列。将数字卡片换成电子自旋,该谜题就可以被用来解释永久磁铁的原理(来源:Quanta Magazine)
15 谜题是个简单的游戏:在一个 4 乘 4 的框架内,有 15 个写着数字1-15 的卡片,玩家的任务是移动卡片,让 15 张卡片按自然数顺序排列。
这个游戏与古老的中国民间益智游戏华容道很像,约翰·霍普金斯大学助理教授李易告诉 DeepTech,“(卡片)形状不太一样,在游戏精髓上是一样。”
今天看来,15 谜题可能有点过时,但在 1880 年可不是这样。当时媒体称:“再多动的孩子和再古板的成人都无法抵抗绞尽脑汁解决 15 谜题的诱惑。”不过数学家最终证明:只有一半的卡片组合方式最终可以通过移动实现顺序排列。
140年后的今天,15 谜题再度引起了科学家的兴趣,因为它有助于解释一个更加复杂的谜题:磁铁为什么会产生磁力?
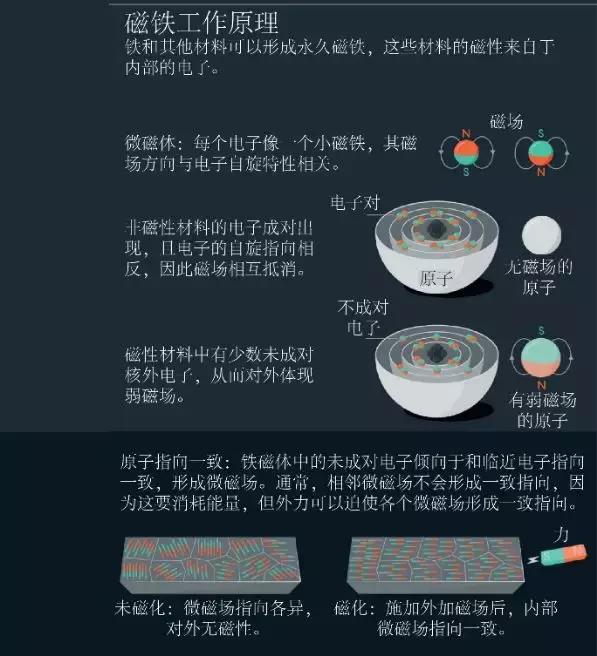
永久磁铁是一种铁磁性材料,这种材料的所有电子自旋方向一致,从而产生磁场。具体来说,铁、钴和镍具有巡游铁磁性,即内部电子可以自由运动。每个电子具有自己的磁矩,但若要解释为何所有电子的磁矩能实现方向一致,则需要计算所有电子之间的复杂量子互动,这种工作太过复杂以致几乎不可能完成。
李易表示,“巡游铁磁性是凝聚态物理中最复杂的理论问题之一。”
不过,借助 15 谜题中的数学工具,李易与她的研究生 Eric Bobrow 和数学系研究生 Keaton Stubis 向着解决该问题迈进了一步。他们近期在 Physical ReviewB 发表的论文将 15 谜题的数学原理推广到更普遍、更现实的系统,该工作可能给出对金属磁性起源的更深的理解。
加州大学圣地亚哥分校的物理学家 Daniel Arovas 表示,该工作非常值得赞赏。此外,由于巡游铁磁性的理论工作很少,因此他个人非常喜欢这项工作。
空穴之舞电子在金属中需要服从两项基本约束。第一,电子带负电,因此相互排斥。第二,电子必须服从泡利不相容原理,即:2 个粒子不能占据同一个量子态。也就是说,相同自旋方向——自旋与电子磁矩有关——的电子,不能在同一个原子核周围占据同一个量子态,但是 2 个自旋方向相反的电子可以。
根据以上 2 个约束,大批自由电子最容易出现的状态是彼此分离,且自旋方向一致,此时金属对外体现出铁磁性。
(来源:Quanta Magazine)
但这只是解释了结果,而长期困扰物理学家的问题是:如此有序的微观结构是如何通过电子之间的不计其数的量子互动产生的?李易进一步解释,一个电子的量子运动——其量子特性的复杂数学描述——可以跟另一个电子的量子运动发生关联。为了精确地描述一群电子如何产生铁磁性,你必须对它们做一个整体性描述,因为每一个电子不停地被其他电子的量子运动通过相互作用而关联。事实上,想用严格的数学公式来描述这种复杂的量子关联是很少能达到的。
李易团队选择的方法是,研究一个更简单,但能表现铁磁性基本物理性质的模型。事实上,李易的工作是某项 50 多年前的里程碑工作的拓展。
剑桥大学物理学家、2016 年物理学诺奖得主大卫·索利斯(David Thouless)和来自名古屋大学、当时在加州大学圣地亚哥分校访问的物理学家长冈洋介(Yosuke Nagaoka)分别于 1965 和 1966 年独立发表了自己的工作,这项工作日后被称为长冈-索利斯理论。该理论基于一个理想化的原子晶格模型。尽管这一理论成立的前提条件与现实中的金属磁性现象的条件并不一致,其重要性一方面在于第一次解释了电子自旋方向为什么会达成一致,另一方面在于该工作的数学证明避免了物理上的近似,确保了精确性。
想象一个 2 维网格。该网格中的每个节点可以容纳 2 个自旋方向相反的电子,但该理论假定:让 2 个电子占据同一个节点所需要的能量是无穷大,因此实际上每个节点中最多只有 1 个电子。每个电子的自旋方向只有“上”或“下”两种取值。每个电子的自旋方向不是固定的,因此该模型未必会对外显示出铁磁性。

图丨李易(来源:Johns Hopkins University)
现在,从模型中移除 1 个电子,从而产生一个空穴。相邻电子可以进入这个空穴,把自己原先的位置变成空穴。另一个电子可以进入这个新空穴,产生另一个空穴。如此这般,空穴在各个节点之间运动。长冈和索利斯发现,加入 1 个空穴,就足以让剩下的所有电子的自旋方向一致,因为这种状态——铁磁性状态——是最低能态。
另一方面,为了让整个模型处于最低能态,空穴自由运动的同时,不能扰动电子自旋格局,因为这种行为会需要额外的能量。为了让电子的运动不影响自旋格局,所有电子的自旋方向必须一致。
东京大学物理学家押川正毅(Masaki Oshikawa)表示,长冈理论是少数几个可以解释铁磁性现象的模型,但该模型离真实情况仍然太过遥远。
例如,该模型强行设定,2 个电子居于同一个节点需要耗费无穷大的能量。但在真实磁体中,这种行为的能量消耗不是无穷大——尽管仍然不小。此外,长冈-索利斯模型只能适用于 2 维正方和三角网格,以及 3 维立方网格,但现实存在的铁磁性金属,其晶格结构类型丰富得多。
如果长冈-索利斯理论真的是铁磁性原理的正确物理解释,那么必须证明其适用于更多类型的晶格结构。李易表示,长期以来物理学家看好该理论的普适性,但一直没有得到合适的证明。
自旋和数字卡片1989年,日本学习院大学物理学家田崎晴明(Hal Tasaki)证明,长冈-索利斯理论在具备连通性的网格中都可以成立。
什么是连通性?如果这个网格在产生 1 个空穴之后,你无需改变自旋方向向上和向下的电子数目,就可以通过移动电子,构成所有可能的电子空间排布,则这个网格满足连通性。
但是没人能证明,2 维正方和三角网格,以及 3 维立方网格之外的网格结构也服从连通性,所以这个理论的普适性仍然存在问题。
李易先将初步研究目标设定在解析证明六边形蜂窝状晶格的连通性。与她的物理系研究生 Bobrow 讨论后,很快证明了这一命题。进一步,李易的研究生 Bobrow 和他的数学系室友Stubis 意识到:19 世纪的 15 谜题游戏要解决的问题跟长冈-索利斯问题可能有相通之处。在进一步的讨论中,李易和研究生 Bobrow 认识到只要把卡片上的数字换成"上"和"下"自旋,该谜题就变成类似长冈-索利斯问题——1 个空穴在原子晶格中运动。
如果你能让 15 个数字恢复顺序,那么这个谜题就被解开,而这正是连通性的定义。因此“给定网格是否满足连通性”的问题,被转化为“等价网格谜题是否可解”的问题。
1974年,加州理工数学家Richard Wilson 找到了判定对任一网格形态是否存在求解广义 15 谜题的方法。作为证明的一部分,他指出,对于几乎所有的非可再分网格(即移走 1 个电子之后,各个节点间仍然保持互联的网格),玩家都可以通过移动卡片生成自己要想的排列,只要移动步数是偶数。少数不符合这个规律的网格是边数多于 3 的单个多边形网格,以及一个格点位于一个六边形的中心并连接 2 个相对顶点的“西塔-0”图。
现在,研究人员可以用 Wilson 的结果来推广长冈-索利斯理论。对于存在 1 个空穴的电子系统,他们证明,几乎所有的网格结构都满足连通性,比如 2 维蜂窝网格和 3 维金刚石网格。而不满足连通性的 2 个例外——单个多边形网格和“西塔-0”图——不存在于现实世界的铁磁性金属中。
下一步的研究加州大学圣克鲁兹分校的物理学家 Sriram Shastry 认为,15 谜题是一个全新的、潜在成果丰硕的研究方向,因为它通过与图论的联系,引入了新的学术语言。物理学和数学的交叉将会在未来导向丰硕的成果。
从李易早期的求学经历看,曾在多个领域学习。她本科一年级时是复旦大学的药学专业,有机化学、生物等课程都很吸引她,成绩也优秀。
但一次偶然的机会,让她迷上了物理学。那天,李易去上化学课,结果教室调换了,她没有接到通知。等到上课了,她才发现是复旦大学物理系金晓峰教授的物理课,当时讲费曼物理学,穿插有很多物理学发展的历史,"觉得很有意思,就旁听了"。第二年,她就想办法转到物理系。
复旦大学的物理系和数学系交流很多。因此,李易也受益于来自数学系老师的学术指导。2009 年,她在复旦大学获物理学硕士学位。2013 年在加州大学圣地亚哥分校获物理学博士学位。随后,在普林斯顿大学从事博士后研究。从 2016 年 7 月起,李易任约翰斯·霍普金斯大学助理教授,主要从事理论凝聚态物理相关研究工作。
2018年,李易获得美国斯隆研究奖物理学奖。该奖设立宗旨是奖励那些在职业生涯早期的杰出年轻学者。
回到铁磁性理论的研究,尽管已经取得了显著进步,但距离问题的最终解决还有很远。首先,空穴运动步长为奇数的时候,长冈-索利斯理论未必成立。此外,空穴数目必须等于 1,不能多也不能少,这显然不符合事实。在金属中,空穴数量非常庞大,甚至会占据大部分晶格结构节点。
下一步,物理学家尝试将长冈-索利斯理论推广到多空穴系统。通过数值计算,有迹象显示,有限尺寸的正方网格中,若有不超过20% 的空穴,长冈铁磁体理论看上去仍然成立。基于田光善和沈顺清曾逐步发展的方法,李易研究组进一步证明了在无限大的 2 维蜂窝网格和 3 维金刚石网格中,只要空穴数目不超过蜂窝网格总节点数的二分之一次方,或者金刚石网格总节点数的五分之二次方,长冈铁磁体仍然可以存在。
李易认为,以上研究可望引出更能真实描述巡游铁磁性的模型。“它们不过是未来研究物理上更实际模型的起点。”
,





