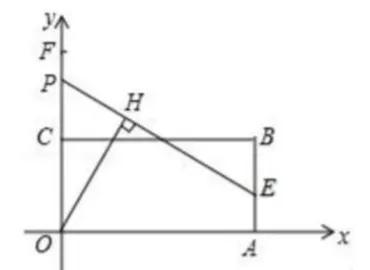
例:如图,矩形OABC的边OA,OC分别在x轴,y轴上,点B坐标(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,点P从点F(0,25/4)运动到原点O的过程中,求点H运动路径长?
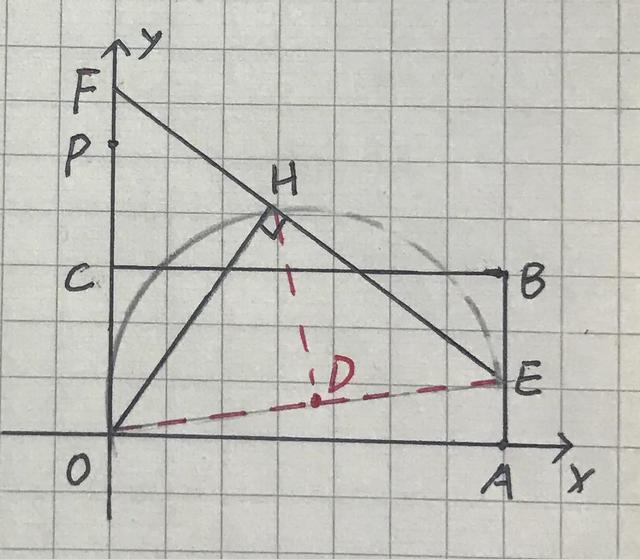
分析:连接OE,Rt△OAE中
OE²=OA² AE²=7² 1²
∴OE=5√2,且∠OHE=90°
∴点H运动轨迹:以1/2.OE为半径,以D点为圆心的⊙D部分弧上运动(定弦定角)
当动点P:位于点F时
S△OEF=1/2×25/4×7=175/8
易求:EF²=(25/4−1)² 7²
∴EF=35/4
∵S△OEF=1/2EF.OH
∴1/2×35/4×OH=175/8
∴OH=5
Rt△OEH中:sin∠OEH=OH/OE=√2/2
∴∠OEH=45°,
即:点H运动所对应圆心角∠ODH=90°
∴点H运动路径长:
(90°×π×5√2/2)/180°=5√2π/4。
,




