
你好,我是方山
01"安培力是洛伦兹力的宏观表现,洛伦兹力是安培力的微观本质",这句话是很多老师会告诉学生的,也有很多资料书上对于它们两者的关系,也是这么一句话进行介绍。
但是细心的你如果仔细细想,就会发现这里存在一个超级大bug。下面我来讲这个bug是什么,以及解决这个bug后,我们对于安培力、洛伦兹力会有一个怎样的全新认识。
咱们先来说说安培力,安培力的大小为

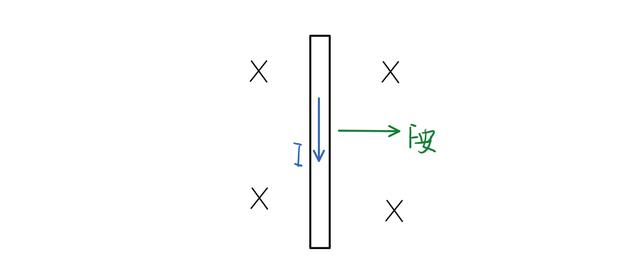
安培力的方向可以根据左手定则判断出来,如下图所示,这根导体杆的安培力的方向向右,那么这根导体棒就会向右运动,安培力对它会做正功
接着来说说洛伦兹力,洛伦兹力的大小为

洛伦兹力的方向也可以根据左手定则判断出来,如下图所示,这个正电粒子的洛伦兹力的方向总是与其速度方向垂直,洛伦兹力对它永不做功

Bug就在这里,既然安培力可以做功,而洛伦兹力永不做功,不做功的洛伦兹力通过多次累加就可以做功了?
那为什么说安培力是洛伦兹力的宏观表现呢?
这个显然解释不通。因此,我们需要重新的审视文章开始那句话。
02我先来解释一下文章开头那句话是怎么来的。
1)导体电流微观表达式
假设一段导体的单位体积内的自由电荷数为n,每个自由电荷所带的电荷量为q,导体的横截面积为S,自由电荷数定向移动的速度为v。
电流的原始定义为I=Q/t,这个式子的本质含义是单位时间内流过导体某横截面积的电荷量大小就是电流的大小。
如下图所示,我们取这段导线中绿颜色的截面来进行研究

则可根据电流的定义式求出这段导体电流的微观表示式

2)安培力与洛伦兹力关系推导
我们现将这段通电导体放入一个方向朝纸面内的匀强磁场中,如图所示

那么,每一个定向移动的电荷所受的洛伦兹力的方向向下,大小为

假设这个导体长度为L,那么整段导体中所有的自由电荷所有的洛伦兹力综合为

从这里的推导可以看到我们文章开始说的那句话,"安培力是洛伦兹力的宏观表现,洛伦兹力是安培力的微观本质"。
03但是到这里,还没有解释那个开始我们说的那个bug,我们接着来建模分析。、
1)(电动机模型)给导线通电流,导线刚开始是静止的,忽略一切摩擦
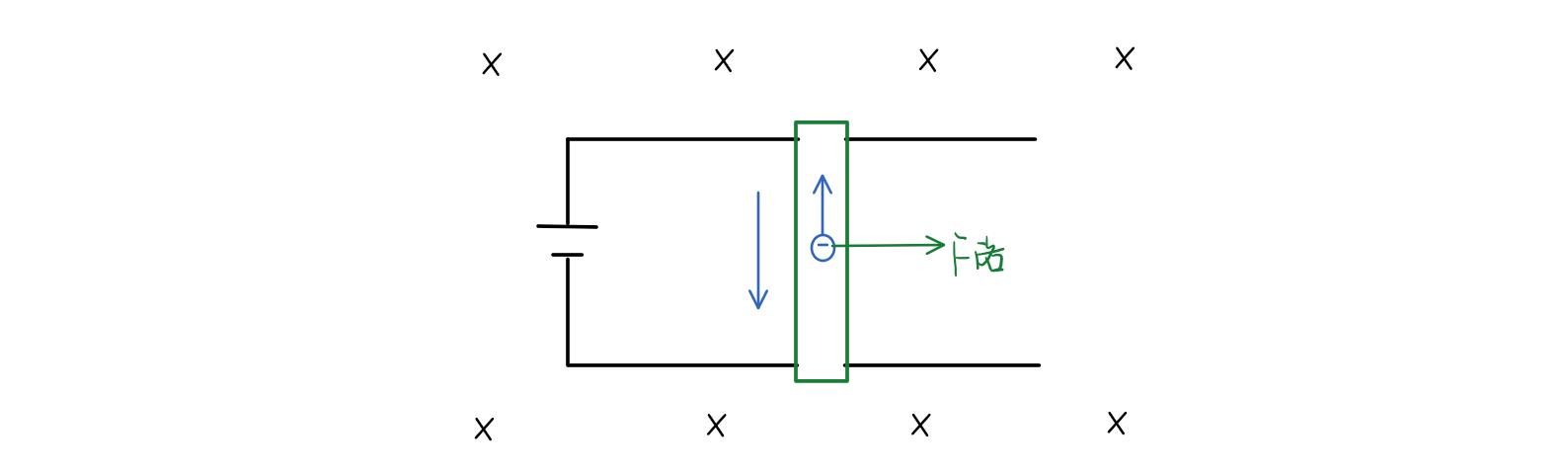
刚开始,导体杆静止,导体杆里面的有向下的电流,意味着导体杆里面有向上定向移动的自由电子,这些电子受到向右的洛伦兹力,每个自由电子受到的洛伦兹力的和就是宏观表现出来的安培力,这个安培力就促使导体棒向右开始运动。
假若导体杆运动起来后,有一个向右的速度v1,导体杆里面的自由电荷定向移动的速度为v2,那么导体杆里面的自由电荷实际的运动速度方向是两个速度的叠加,具体的看下图分析。

导体杆向右移动的速度v1(当然,这也是自由电子向右移动的速度),产生了一个向下的洛伦兹力F洛1。自由电子向上沿着导体杆定向移动的速度v2,产生了一个向右的洛伦兹力F洛2。
每个自由电子所受的洛伦兹力F洛2的合力就是宏观的安培力,每个自由电子所受的洛伦兹力F洛1,在阻碍电子沿着导体杆定向移动,也就是说产生了一个反向的电动势。
现在设F洛2的宏观安培力做功为W2,F洛1的宏观反电动势做功为W1
重点的来了:由于洛伦兹力不做功,所以,W1 W2=0。
也就可以推理如下式子

由此,我们可以知道这个模型中整个能量的分配关系如下

反向电动势在消耗电能,这部分消耗的电能,都转化到了导体杆的动能上去(增加了导体杆的机械能)。
本质上讲,是洛伦兹力起到了将电能转化为机械能的桥梁。
2)(发电机模型)不给导体通电,导体杆有初速度v1,忽略一切摩擦

由于导体杆具有向右的初速度v1,那么自由电荷就会受到向下的洛伦兹力F洛1,这个力会使得自由电荷沿着导体杆向下移动,假设移动向下定向移动的速度为v2,那么自由电荷就会受到一个想左的洛伦兹力F洛2。
这个F洛2的宏观表现就是导体杆所受的安培力,F洛1的宏观表现就是产生了感应电动势,由于洛伦兹力不做功,所以,W1 W2=0。
由此,我们可以得到这个模型的能量分配如下

导体杆克服了安培力做功,而安培力做功的大小等于产生的感应电动势做功的大小,也就是说,动能全部转化成了电能,然后这部分电能会通过电阻,通过电阻后就会生热
所以,最终的关系就是导体杆的动能,全部转化成了电阻的热量耗散。本质上讲,还是由于洛伦兹力起到的桥梁作用。
04我对本文的内容进行复盘总结:
①"安培力是洛伦兹力的宏观表现,洛伦兹力是安培力的微观本质",这句话无法解释安培力可以做功,但是洛伦兹力永不做功的问题;
②我推推导了安培力与洛伦兹力的表达式之间的关系;
③我引入了两种模型,一个是电动机模型,一个是发电机模型,从本质上讲解了洛伦兹力与安培力的关系:
洛伦兹力垂直于导体杆的分力的合力才是安培力;洛伦兹力沿着导体杆的分力的合力产生了感应电动势,并且可以知道安培力做功=感应电动势做功,洛伦兹力在机械能与电能之间起到了桥梁作用。
这篇文章我已经尽力的写的通俗,但是理解起来还是需要你花一点点功夫琢磨一下,但是请相信我,花这点时间搞清楚本文的内容,是很值得的。
,




