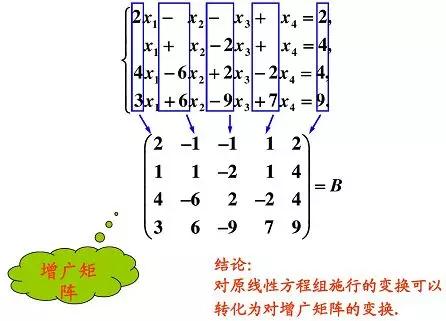
矩阵的初等变换有这样一个性质:
设A是一个m×n矩阵,对A施行一次初等行变换,相当于在A的左边乘相应的m阶初等矩阵;对A施行一次初等列变换,相当于在A的右边乘相应的n阶初等矩阵。
这个性质的内容其实描述的是m阶(或n阶)初等矩阵“教”m×n矩阵“做事”的过程。
为了说明这个事情,首先回忆一下单位矩阵、初等矩阵和初等变换的概念。
单位矩阵:是指主对角线上的元素均是1,其余元素都是0的方阵。m行(列数与行数相等)的单位矩阵,就叫做m阶单位矩阵。
三种初等行(列)变换:
1.对换两行(或者两列);
2.以数k≠0乘某一行(或某一列)的全部元素;
3.把某一行(或某一列)所有元素的k倍加到另一行(列)对应的元素上去。
初等矩阵:由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵。
下面分两种情况来说明这个问题。
第一种情况:
A是一个m×n矩阵(m行n列),B是由m阶单位矩阵经过一次初等行变换得到的,在A的左边乘以初等矩阵B,相当于对A实施一次初等行变换。这种变换的过程是完全仿照m阶单位矩阵变化为矩阵B的过程来的。
如果B是由m阶单位矩阵对调第i行和第j行得到的,那么矩阵C=BA其实就是把矩阵A的第i行和第j行对调。例子:

如果B是由m阶单位矩阵第i行乘k得到的,那么矩阵C=BA其实就是把矩阵A的第i行乘k。例子:
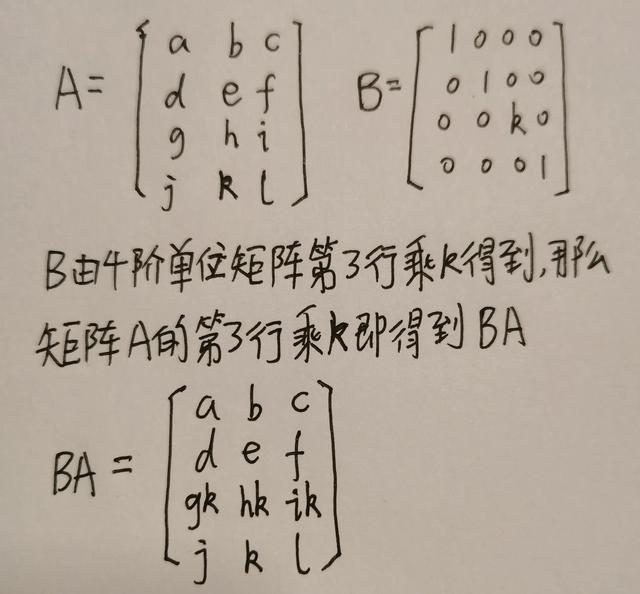
如果B是由m阶单位矩阵第i行的元素乘k加到第j行相应元素上得到的,那么矩阵C=BA其实就是把矩阵A的第i行的元素乘k加到第j行相应元素上。例子:
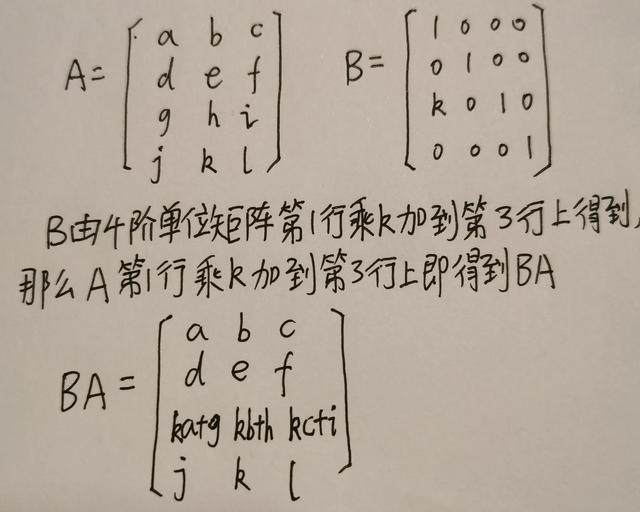
对于第一种情况,为了方便记忆,我们可以假想下述一个情景对话。B对C(C=BA)说:“我是由m阶单位矩阵经过一次初等行变换得到的,那你就在矩阵A基础上做一次相同的初等行变换就能得到你自己了。”B就是这样教C做事的。
第二种情况:
A是一个m×n矩阵(m行n列),B是由n阶单位矩阵经过一次初等列变换得到的,在A的右边乘以初等矩阵B,相当于对A实施一次初等列变换。这种变换的过程是完全仿照n阶单位矩阵变化为矩阵B的过程来的。
如果B是由n阶单位矩阵对调第i列和第j列得到的,那么矩阵C=AB其实就是把矩阵A的第i列和第j列对调。例子:

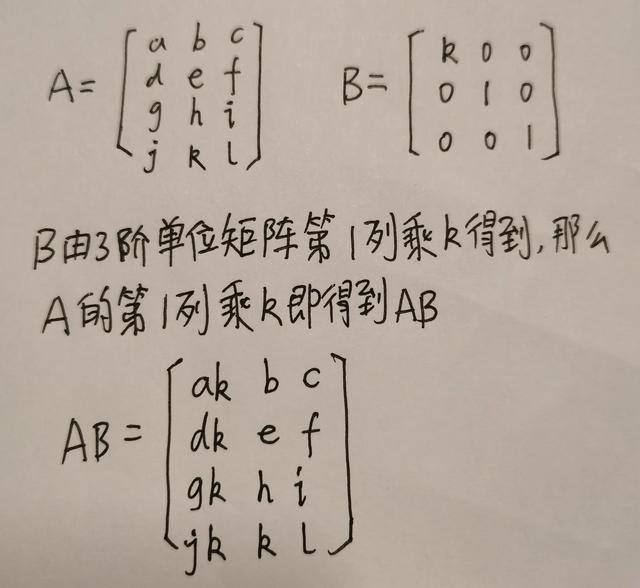
如果B是由n阶单位矩阵第i列乘k得到的,那么矩阵C=AB其实就是把矩阵A的第i列乘k。例子:
如果B是由n阶单位矩阵第i列的元素乘k加到第j列相应元素上得到的,那么矩阵C=AB其实就是把矩阵A的第i列的元素乘k加到第j列相应元素上。例子:

对于第二种情况,为了方便记忆,我们可以假想下述一个情景对话。B对C(C=AB)说:“我是由n阶单位矩阵经过一次初等列变换得到的,那你就在矩阵A基础上做一次相同的初等列变换就能得到你自己了。”B就是这样教C做事的。
,