↑↑点击上方蓝字把我们置顶/设为星标吧
一起在育儿中精进、成长~

- 这是果爸的2022年第 005期分享 -
今天我们来研究下平行四边形的面积问题,在这个模块中主要涉及两个知识点:
1.两平行线间距离相等;
2.同底(等高)或同高(等底)的三角形面积相等;
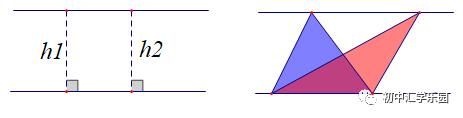
3.面积相关模型

我们来看下今天的3道关于平行线面积转化的3道例题。
首先我们来看下第一题,题目要我们求解△ACP和△PEF面积之差的变化情况,△ACP和△PEF没有任何关联关系,所以我们要找个中间量帮助它们建立联系,我们会发现AB//CD,根据等积变化可以将△ACP的面积转化到△BCP的面积,此时我们会发现△BCP与△PEF三角形的高相等,所以它们的面积差的变化情况等于1/2×h×|BC-EF|相同,又因为BC=AD=EF,所以|BC-EF|=0,面积差等于0,即一直保持不变。

【总结】平行四边形求解面积或者面积关系,常运用到平行线转化面积。
接着我们来看下例2
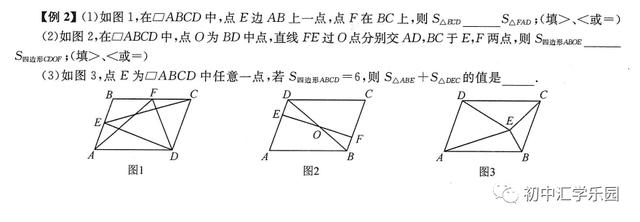
(1)△ECD和S△AFD没有直接关系,所以我们要找个中间量帮助它们建立联系,根据等积变化我们发现这两个三角形的面积都等于S△ACD,也就是整个平行四边形的一半,所以这两个三角形的面积相等。

(2)由于平行四边形是中心对称图形,易得△EOD≌△BOF,则S△EOD=S△BOF,则四边形ABOE=S△ABD-S△EOD,四边形ABOE=S△CBD-S△BOF,即可得到两个四边形面积相等。

(3)根据下左图中的面积关系,易得出S2 S4等于四边形面积的一半,则S△ABE S△DEC=3


接着我们来看下例3,证明角平分线的方法有两种:①两个角相等;②到角两边的距离相等的点在角平分线上;本题运用方法②来求证角平分线,我们会发现△BCE和△FCD的面积相等,且DF=BE,所以可以得出点C到∠BGD两边的距离相等,则GC是∠BGD的角平分线。


加油,明天我们继续!
每天与大家一起努力
培优《平行四边形》例题3解析
培优《平行四边形》例题解析
平行四边形与力学好题分享2
初二数学和初二物理第一周高频选填题推荐
答疑帖:初二数学中位线
,




